题目内容
如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且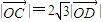 ,
, .若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M.
.若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M.(1)求椭圆M的方程;
(2)过点E的直线l与椭圆M交于不同的两点P,Q,点P在点E,Q之间,且
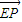 =λ
=λ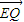 ,求实数λ的取值范围.
,求实数λ的取值范围.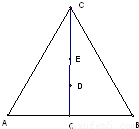
【答案】分析:(1)建立如图所示的直角坐标系,由已知可得D(0,1),E(0,2),则有2c=4,b=1,根据a2=b2+c2可求a,进而可求椭圆的方程
(2)设P(x1,y1)Q(x2,y2),E(0,2),则由 .
. =λ
=λ 可得x1=λx2,y1=λy2-2λ+2,由P,Q都在椭圆上,代入椭圆方程,
可得x1=λx2,y1=λy2-2λ+2,由P,Q都在椭圆上,代入椭圆方程,
可得y2与λ之间的关系,结合-1≤y2≤1,及P在E,Q之间,又 ,可求λ的范围
,可求λ的范围
解答:
解:(1)建立如图所示的直角坐标系,
由于 ,
, ,
, ,
,
∴D(0,1),E(0,2)
设椭圆方程为
∴2c=4⇒c=2,b=1
即椭圆方程为 ;…(6分)
;…(6分)
(2)设p(x1,y1)Q(x2,y2)
∵E(0,2),即 .λ
.λ =
=
∴ ①…(7分)
①…(7分)
又∵P,Q都在椭圆上
∴ ②…(8分)
②…(8分)
由①②得∴
消去x2得 …(10分)
…(10分)
∵-1≤y2≤1,
∴
又∵P在E,Q之间,又 ,
,
∴0<λ<1,
∴λ范围为 .…(12分)
.…(12分)
点评:本题考查了由椭圆的性质求解椭圆的标准方程的求法,求λ的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化.
(2)设P(x1,y1)Q(x2,y2),E(0,2),则由
 .
. =λ
=λ 可得x1=λx2,y1=λy2-2λ+2,由P,Q都在椭圆上,代入椭圆方程,
可得x1=λx2,y1=λy2-2λ+2,由P,Q都在椭圆上,代入椭圆方程,可得y2与λ之间的关系,结合-1≤y2≤1,及P在E,Q之间,又
 ,可求λ的范围
,可求λ的范围解答:

解:(1)建立如图所示的直角坐标系,
由于
 ,
, ,
, ,
,
∴D(0,1),E(0,2)
设椭圆方程为

∴2c=4⇒c=2,b=1

即椭圆方程为
 ;…(6分)
;…(6分)(2)设p(x1,y1)Q(x2,y2)
∵E(0,2),即
 .λ
.λ =
=
∴
 ①…(7分)
①…(7分)又∵P,Q都在椭圆上
∴
 ②…(8分)
②…(8分)由①②得∴

消去x2得
 …(10分)
…(10分)∵-1≤y2≤1,
∴

又∵P在E,Q之间,又
 ,
,∴0<λ<1,
∴λ范围为
 .…(12分)
.…(12分)点评:本题考查了由椭圆的性质求解椭圆的标准方程的求法,求λ的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
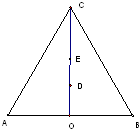 如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且
如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且
