题目内容
下列说法正确的有 :
①对于函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)在区间(a,b)内一定没有零点.
②函数f(x)=2x-x2有两个零点.
③若奇函数、偶函数有零点,其和为0.
④当a=1时,函数f(x)=|x2-2x|-a有三个零点.
①对于函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)在区间(a,b)内一定没有零点.
②函数f(x)=2x-x2有两个零点.
③若奇函数、偶函数有零点,其和为0.
④当a=1时,函数f(x)=|x2-2x|-a有三个零点.
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用
分析:①可取m=n=0,a=-1,b=1,但f(0)=0,即可判断;
②分别画出函数y=x2和y=2x的图象,由图象即可判断;
③由于它们的定义域关于原点对称,故其和为0,即可判断;
④由|x2-2x|=1,解得x=1或x=1±
,即可判断.
②分别画出函数y=x2和y=2x的图象,由图象即可判断;
③由于它们的定义域关于原点对称,故其和为0,即可判断;
④由|x2-2x|=1,解得x=1或x=1±
| 2 |
解答:
 解:①对于函数f(x)=x2+mx+n,
解:①对于函数f(x)=x2+mx+n,
若f(a)>0,f(b)>0,比如m=n=0,a=-1,b=1,但f(0)=0,
故①错;
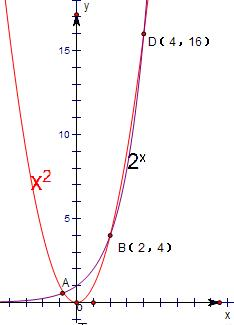
②分别画出函数y=x2和y=2x的图象,如图所示:
由图可知,它们的交点情况是:恰有3个不同的交点,
故②错;
③若奇函数、偶函数有零点,由于它们的定义域关于原点对称,故其和为0,故③对;
④当a=1时,函数f(x)=|x2-2x|-a,由|x2-2x|=1,解得
x=1或x=1±
,故④对.
故答案为:③④.
 解:①对于函数f(x)=x2+mx+n,
解:①对于函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,比如m=n=0,a=-1,b=1,但f(0)=0,
故①错;
②分别画出函数y=x2和y=2x的图象,如图所示:
由图可知,它们的交点情况是:恰有3个不同的交点,
故②错;
③若奇函数、偶函数有零点,由于它们的定义域关于原点对称,故其和为0,故③对;
④当a=1时,函数f(x)=|x2-2x|-a,由|x2-2x|=1,解得
x=1或x=1±
| 2 |
故答案为:③④.
点评:本题考查函数的性质和运用,考查函数的对称性和函数的零点的问题,可以直接解方程或画图象,或运用零点存在定理,属于中档题.

练习册系列答案
相关题目
 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OA=6,则tan∠APO的值为