题目内容
若实数X满足log3x=sinθ+cosθ,其中θ∈[-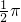 ,0],则函数f(x)=|2x-1|+x的值域为
,0],则函数f(x)=|2x-1|+x的值域为
- A.[
 ,2]
,2] - B.[
 ,8]
,8] - C.[
 ,2]
,2] - D.[
 ,8]
,8]
D
分析:由X满足log3x=sinθ+cosθ,所以x=3sinθ+cosθ= ,又θ∈[-
,又θ∈[-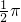 ,0],所以
,0],所以 ,所以
,所以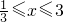 ,又f(x)的表达式可化为f(x)=
,又f(x)的表达式可化为f(x)=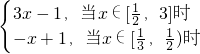 据此可求出函数f(x)=|2x-1|+x的值域.
据此可求出函数f(x)=|2x-1|+x的值域.
解答:∵log3x=sinθ+cosθ,∴x=3sinθ+cosθ= ,
,
又∵θ∈[-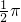 ,0],∴
,0],∴ ,
,
∴
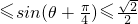 ,即-1≤
,即-1≤
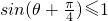 ,
,
∴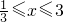 .
.
因此f(x)的表达式可化为
f(x)=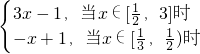
①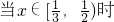 ,
, <-x+1≤
<-x+1≤ ,即
,即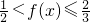 ;
;
②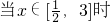 ,
,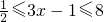 ,即
,即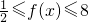 .
.
因此,函数f(x)=|2x-1|+x的值域是[ ,8].
,8].
故选D.
点评:此题考查了对数式化为指数式、指数函数的单调性、三角函数式的化简、三角函数的单调性及值域、含有绝对值类型的函数的值域.熟练掌握上述有关知识及方法是解决此问题的关键.此题还用到了分类讨论的方法去掉绝对值.
分析:由X满足log3x=sinθ+cosθ,所以x=3sinθ+cosθ=
 ,又θ∈[-
,又θ∈[-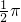 ,0],所以
,0],所以 ,所以
,所以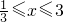 ,又f(x)的表达式可化为f(x)=
,又f(x)的表达式可化为f(x)=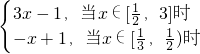 据此可求出函数f(x)=|2x-1|+x的值域.
据此可求出函数f(x)=|2x-1|+x的值域.解答:∵log3x=sinθ+cosθ,∴x=3sinθ+cosθ=
 ,
,又∵θ∈[-
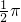 ,0],∴
,0],∴ ,
,∴

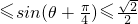 ,即-1≤
,即-1≤
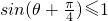 ,
,∴
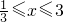 .
.因此f(x)的表达式可化为
f(x)=
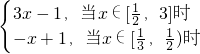
①
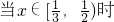 ,
, <-x+1≤
<-x+1≤ ,即
,即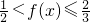 ;
;②
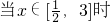 ,
,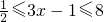 ,即
,即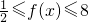 .
.因此,函数f(x)=|2x-1|+x的值域是[
 ,8].
,8].故选D.
点评:此题考查了对数式化为指数式、指数函数的单调性、三角函数式的化简、三角函数的单调性及值域、含有绝对值类型的函数的值域.熟练掌握上述有关知识及方法是解决此问题的关键.此题还用到了分类讨论的方法去掉绝对值.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目