题目内容
如图,已知正三棱柱ABC-A1B1C1底面边长为3,AA1=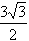 ,D为CB延长线上一点,且BD=BC。
,D为CB延长线上一点,且BD=BC。
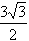 ,D为CB延长线上一点,且BD=BC。
,D为CB延长线上一点,且BD=BC。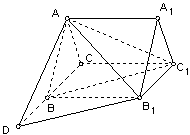
(1)求证:直线BC1∥面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。
| 解:(1)证明:∵CD∥C1B1, 又BD=BC=B1C1, ∴四边形BDB1C1是平行四边形 ∴BC1∥DB1 又DB1  平面AB1D,BC1 平面AB1D,BC1 平面AB1D 平面AB1D ∴直线BC1∥平面AB1D。 |
|
|
(2)过B作BE⊥AD于E,连结EB1, |
 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 AC=
AC=


 =
= =
=


 。
。 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为