题目内容
已知函数 ,
, .
.
(Ⅰ)若函数 和函数
和函数 在区间
在区间 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有唯一解,求实数
有唯一解,求实数 的值.
的值.
【答案】
(1) ;(2)
;(2) .
.
【解析】(1)由已知中函数 ,
, 的解析式,我们易求出他们导函数的解析式,进而求出导函数大于0的区间,构造关于a的不等式,即可得到实数a的取值范围;
的解析式,我们易求出他们导函数的解析式,进而求出导函数大于0的区间,构造关于a的不等式,即可得到实数a的取值范围;
(2)若方程f(x)=g(x)+m有唯一解,则函数h(x)=f(x)-g(x)= 与y=m的图象有且只有一个交点,求出h'(x)后,易求出函数的最值,分析函数的性质后,即可得到满足条件的实数m的值.
与y=m的图象有且只有一个交点,求出h'(x)后,易求出函数的最值,分析函数的性质后,即可得到满足条件的实数m的值.
解:(Ⅰ) 

当 时,
时, ,当
,当 时,
时, ,
,
要使 在
在 上递增,必须
上递增,必须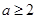

如使 在
在 上递增,必须
上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数 ……………6分
上均为增函数 ……………6分
(Ⅱ)方程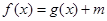 有唯一解
有唯一解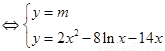 有唯一解
有唯一解
设
 (
( )
)
 随
随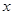 变化如下表
变化如下表
|
|
|
|
|
|
|
|
|
|
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为
的最小值为 ,
,
当 时,方程
时,方程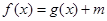 有唯一解. ……14分
有唯一解. ……14分

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|







