题目内容
5．已知复数z满足（1+i）z1=-1+3i，z2=a-i，其中i为虚数单位，a∈R若|z1-$\overline{{z}_{1}}$|＜|z1|．（1）求z1；
（2）求a的取值范围．
分析 （1）利用复数的除法运算法则化简求解即可．
（2）利用复数的模以及不等式，求解即可．
解答 （本小题满分10分）
解：（1）（1+i）z1=-1+3i，z1=$\frac{-1+3i}{1+i}$=$\frac{（-1+3i）（1-i）}{（1+i）（1-i）}$=1+2i．
（2）z2=a-i，$\overline{{z}_{2}}$=a+i，
|z1-$\overline{{z}_{2}}$|=$\sqrt{{a}^{2}-2a+2}$，|z1|=$\sqrt{5}$，
∴$\sqrt{{a}^{2}-2a+2}＜\sqrt{5}$，
∴-1＜a＜3．
点评 本题考查复数的除法运算法则的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
15．已知函数f（x）=$\frac{x}{{e}^{x}}$（x∈R），若x1≠x2，且f（x1）=f（x2），则x1，2-x2大小关系是（ ）
| A． | x1＞2-x2 | B． | x1＜2-x2 | ||
| C． | x1=2-x2 | D． | x1与2-x2大小不确定 |
16．
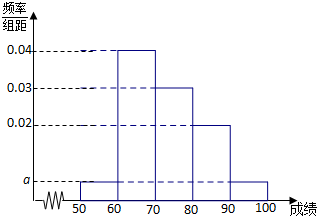某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
某校1000名学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．（1）求图中a的值；
（2）根据频率分布直方图，估计这1000名学生数学成绩的平均分；
（3）若这1000名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如表所示，求语文成绩在[50，90）之外的人数．
| 分数段 | [50，60） | [60，70） | [70，80） | [80，90） |
| x：y | 1：1 | 4：5 | 3：2 | 2：1 |
14．如果函数y=3sin（2x+ϕ）的图象关于点$（\frac{π}{3}，0）$中心对称，那么ϕ的一个值可以为（ ）
| A． | $\frac{π}{3}$ | B． | $-\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $-\frac{π}{6}$ |