题目内容
已知x,y∈Z,n∈N*,设f(n)是不等式组
|
分析:本题考查的知识点是线性规划与归纳推理,我们可以根据约束条件,画出可行域,利用数形结合,分析图象,给出f(1)及f(2)的值,现根据f(1)、f(2)的值,进行归纳总结,推断出f(n)的表达式.
解答: 解:根据约束条件画出可行域如右图:
解:根据约束条件画出可行域如右图:
当n=1时,可行域内的整点只有(1,0)点,
∴f(1)=1,
当n=2时,可行域内的整点有(1,0)、(2,0)、(1,1),
∴f(2)=3,
…
由此可归纳出f(n)=1+2+3+…+n=
故答案为:1,3,
 解:根据约束条件画出可行域如右图:
解:根据约束条件画出可行域如右图:当n=1时,可行域内的整点只有(1,0)点,
∴f(1)=1,
当n=2时,可行域内的整点有(1,0)、(2,0)、(1,1),
∴f(2)=3,
…
由此可归纳出f(n)=1+2+3+…+n=
| n(n+1) |
| 2 |
故答案为:1,3,
| n(n+1) |
| 2 |
点评:要判断可行域内整数可行解的个数,我们可以根据约束条件画出可行域,然后根据图象,结合数形分析的思想,进行判断,如果某个点与可行域的边界的关系很难确定,也可以将该点坐标代入边界直线的方程,根据所得的符合,对点的位置进行判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
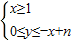 ,表示的平面区域内可行解的个数,由此可推出f(1)=1,f(2)=3,…,则f(10)=( )
,表示的平面区域内可行解的个数,由此可推出f(1)=1,f(2)=3,…,则f(10)=( )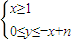 表示的平面区域内可行解的个数,则f(1)= ;f(2)= ;f (n)=
表示的平面区域内可行解的个数,则f(1)= ;f(2)= ;f (n)=