题目内容
已知x,y∈Z,n∈N*,设f(n)是不等式组
,表示的平面区域内可行解的个数,归纳推理f(n)=
.
|
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
分析:根据约束条件,画出可行域,利用数形结合,求出f(1)及f(2)的值,根据f(1)、f(2)的值,进行归纳总结,推断出f(n)的表达式.
解答:解:根据约束条件画出可行域如右图:
当n=1时,可行域内的整点只有(1,0)点,∴f(1)=1,
当n=2时,可行域内的整点有(1,0)、(2,0)、(1,1),∴f(2)=3,
…
由此可归纳出f(n)=1+2+3+…+n=
故答案为:

当n=1时,可行域内的整点只有(1,0)点,∴f(1)=1,
当n=2时,可行域内的整点有(1,0)、(2,0)、(1,1),∴f(2)=3,
…
由此可归纳出f(n)=1+2+3+…+n=
| n(n+1) |
| 2 |
故答案为:
| n(n+1) |
| 2 |
点评:本题考查线性规划知识,考查归纳推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
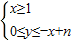 ,表示的平面区域内可行解的个数,由此可推出f(1)=1,f(2)=3,…,则f(10)=( )
,表示的平面区域内可行解的个数,由此可推出f(1)=1,f(2)=3,…,则f(10)=( )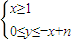 表示的平面区域内可行解的个数,则f(1)= ;f(2)= ;f (n)=
表示的平面区域内可行解的个数,则f(1)= ;f(2)= ;f (n)=