题目内容
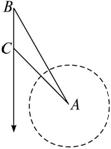
如图所示,海中小岛A周围55海里内有暗礁,船向正南航行,在B处测得小岛A在船的南偏东30°,船行40海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?(参考数据,
≈1.41,
≈1.73)
| 2 |
| 3 |
分析:法一:过A作AE⊥BC于点E.在△ABC中,由正弦定理求出AC,然后求出AE,AE是否小于55,判断有无触礁的危险.
法二:过A作AE⊥BC于点E.在RT△ACE中,求出AE,AE是否小于55,判断有无触礁的危险.
法二:过A作AE⊥BC于点E.在RT△ACE中,求出AE,AE是否小于55,判断有无触礁的危险.
解答: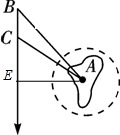 解:法一:过A作AE⊥BC于点E.
解:法一:过A作AE⊥BC于点E.
在△ABC中,BC=40,∠B=30°,
∠ACB=180°-45°=135°,
∠BAC=180°-(30°+135°)=15° …(2分)
由正弦定理可知:
=
∴AC=
=
=80•cos15°=80•cos(60°-45°)
=80•
=20(
+
)…(6分)
∴A到BC所在直线的距离 AE=ACsin45°≈20×(1.73+1)=54.6(海里)<55海里…(10分)
∴小船继续向南航行有触礁的危险.…(12分)
法二:过A作AE⊥BC于点E.在△ABC中,BC=40,∠B=30°
在RT△ACE中,∠ACE=45°∴AE=CE,…(4分)
∴在RT△ACE中有
=tan∠ABE,即
=
…(10分)
解得AE=
=
=20(
+1)≈54.6海里 …(10分)
∴A到BC所在直线的距离d<55海里
∴小船继续向南航行有触礁的危险.…(12分)
 解:法一:过A作AE⊥BC于点E.
解:法一:过A作AE⊥BC于点E.在△ABC中,BC=40,∠B=30°,
∠ACB=180°-45°=135°,
∠BAC=180°-(30°+135°)=15° …(2分)
由正弦定理可知:
| BC |
| sin∠BAC |
| AC |
| sin∠B |
| BC•sin∠B |
| sin∠BAC |
| 40×sin30° |
| sin15° |
=80•
| ||||
| 4 |
| 6 |
| 2 |
∴A到BC所在直线的距离 AE=ACsin45°≈20×(1.73+1)=54.6(海里)<55海里…(10分)
∴小船继续向南航行有触礁的危险.…(12分)
法二:过A作AE⊥BC于点E.在△ABC中,BC=40,∠B=30°
在RT△ACE中,∠ACE=45°∴AE=CE,…(4分)
∴在RT△ACE中有
| AE |
| BC+CE |
| AE |
| 40+AE |
| ||
| 3 |
解得AE=
40
| ||
3-
|
| 40 | ||
|
| 3 |
∴A到BC所在直线的距离d<55海里
∴小船继续向南航行有触礁的危险.…(12分)
点评:此题考查了正弦、余弦定理,以及两角和与差的余弦函数公式,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目