题目内容
如图所示,海中小岛A周围38 n mile内有暗礁,船向正南航行,在B处测得小岛A在船的南偏东30°,船行30 n mile后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?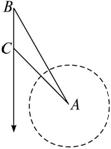
解析:在△ABC中,BC=30,B=30°,∠ACB=180°-45°=135°,
∴∠A=15°.由正弦定理可知![]() =
=![]() .
.
∴![]() =
=![]() .
.
∴AC=![]() =60cos15°=60cos(45°-30°)=60(cos45°cos30°+sin45°sin30°)=15(
=60cos15°=60cos(45°-30°)=60(cos45°cos30°+sin45°sin30°)=15(![]() +
+![]() ).
).
于是A到BC所在直线的距离为ACin45°=15(![]() +
+![]() )·
)·![]()
=15(![]() +1)≈15(1.732+1)
+1)≈15(1.732+1)
=15×2.732=40.98(n mile).
它大于38 n mile,所以继续向南航行无触礁的危险.
点评:在运用解三角形知识解决有关实际问题时,要注意阅读理解,弄清题意,特别要弄清类似于方位角等术语的含义.画出示意图,分析与解决问题有关的三角形,利用正、余弦定理求解.

练习册系列答案
相关题目

