题目内容
19.已知f(x)是R上的偶函数,若在区间(-∞,0)上f′(x)>0,且有f(a+1)<f(2a-1),则实数a的取值范围是(0,2).分析 由导数与函数单调性的关系、偶函数的性质判断出f(x)的单调性,将f(a+1)<f(2a-1)等价转化,列出关于a的不等式,求出实数a的取值范围.
解答 解:因为在区间(-∞,0)上f′(x)>0,
所以f(x)在区间(-∞,0)上单调递增,
因为f(x)是R上的偶函数,
所以f(x)在(0,+∞)上单调递减,
则f(a+1)<f(2a-1)等价于f(|a+1|)<f(|2a-1|),
所以|a+1|>|2a-1|,两边平方得0<a<2,
所以实数a的取值范围是(0,2),
故答案为(0,2).
点评 本题考查导数与函数单调性的关系、偶函数的性质,以及转化思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.“若随机事件A,B相互独立,则P(A∩B)=P(A)P(B)”的逆否命题是( )
| A. | “若随机事件A,B相互不独立,则P(A∩B)≠P(A)P(B)” | |
| B. | “若随机事件A,B相互独立,则P(A∩B)≠P(A)P(B)” | |
| C. | “若P(A∩B)=P(A)P(B),则随机事件A,B相互不独立” | |
| D. | “若P(A∩B)≠P(A)P(B),则随机事件A,B相互不独立” |
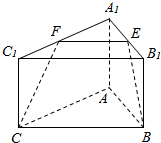 如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?
如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?