题目内容
若不同直线l1,l2的方向向量分别为
,
,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是( )
| μ |
| v |
分析:两直线的平行与垂直可转化为其方向向量的平行与垂直,进而转化为向量间的运算.
解答:解:因为μ•v=(1,2,-1)•(0,2,4)=0+2×2-1×4=0,所以μ⊥v,即l1⊥l2,故排除A;
由μ=(0,2,-3),v=(0,-2,3),得μ=-v,所以μ∥v,即l1∥l2,故排除C;
因为μ•v=(1,6,0)•(0,0,-4)=1×0+6×0+0×(-4)=0,所以μ⊥v,即l1⊥l2,故排除D;
μ=(3,0,-1),v=(0,0,2),因为μ与v既不平行也不垂直,所以l1与l2既不平行也不垂直;
故选B.
由μ=(0,2,-3),v=(0,-2,3),得μ=-v,所以μ∥v,即l1∥l2,故排除C;
因为μ•v=(1,6,0)•(0,0,-4)=1×0+6×0+0×(-4)=0,所以μ⊥v,即l1⊥l2,故排除D;
μ=(3,0,-1),v=(0,0,2),因为μ与v既不平行也不垂直,所以l1与l2既不平行也不垂直;
故选B.
点评:本题考查空间向量的数量积运算及其应用,空间直线间的位置关系可转化为它们方向向量间的运算解决.

练习册系列答案
相关题目
 ,
,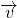 ,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是
,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是 ,
, ,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是( )
,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是( ) =(1,2,-1),
=(1,2,-1), =(0,2,4)
=(0,2,4) =(3,0,-1),
=(3,0,-1), =(0,0,2)
=(0,0,2) =(0,2,-3),
=(0,2,-3), =(0,-2,3)
=(0,-2,3) =(1,6,0),
=(1,6,0), =(0,0,-4)
=(0,0,-4) ,
, ,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是( )
,则下列下列选项中满足直线l1,l2中既不平行也不垂直的条件是( ) =(1,2,-1),
=(1,2,-1), =(0,2,4)
=(0,2,4) =(3,0,-1),
=(3,0,-1), =(0,0,2)
=(0,0,2) =(0,2,-3),
=(0,2,-3), =(0,-2,3)
=(0,-2,3) =(1,6,0),
=(1,6,0), =(0,0,-4)
=(0,0,-4)