题目内容
不等式x2+ax+a+2≥0对一切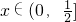 恒成立,则a的最小值是
恒成立,则a的最小值是
- A.-2
- B.

- C.1
- D.2
B
分析:f(x)=x2+ax+a+2对称轴为x=- 分三种情况讨论:(1)当-
分三种情况讨论:(1)当- ≤0时,解得a≥0;(2)当0<-
≤0时,解得a≥0;(2)当0<- ≤
≤ 时,解得-1≤a≤0;(3)当-
时,解得-1≤a≤0;(3)当- >
> 时,解得
时,解得 .由此能求出a的最小值.
.由此能求出a的最小值.
解答:f(x)=x2+ax+a+2对称轴为x=- 分三种情况讨论
分三种情况讨论
(1)当- ≤0时,f(0)=a+2≥0,即a≥-2,
≤0时,f(0)=a+2≥0,即a≥-2,
∴a≥0
(2)当0<- ≤
≤ 时,f(-
时,f(- )=-
)=- +a+2≥0
+a+2≥0
即2-2 ≤a≤2+2
≤a≤2+2 .
.
∴-1≤a≤0.
(3)当- >
> 时,f(
时,f( )=
)= +
+ +a+2≥0
+a+2≥0
∴ .
.
综上所述,a的最小值- .
.
故选B.
点评:本题考查二次函数的性质和应用,解题时要认真审题,仔细解答,注意对称轴性质的合理运用.
分析:f(x)=x2+ax+a+2对称轴为x=-
 分三种情况讨论:(1)当-
分三种情况讨论:(1)当- ≤0时,解得a≥0;(2)当0<-
≤0时,解得a≥0;(2)当0<- ≤
≤ 时,解得-1≤a≤0;(3)当-
时,解得-1≤a≤0;(3)当- >
> 时,解得
时,解得 .由此能求出a的最小值.
.由此能求出a的最小值.解答:f(x)=x2+ax+a+2对称轴为x=-
 分三种情况讨论
分三种情况讨论(1)当-
 ≤0时,f(0)=a+2≥0,即a≥-2,
≤0时,f(0)=a+2≥0,即a≥-2,∴a≥0
(2)当0<-
 ≤
≤ 时,f(-
时,f(- )=-
)=- +a+2≥0
+a+2≥0即2-2
 ≤a≤2+2
≤a≤2+2 .
.∴-1≤a≤0.
(3)当-
 >
> 时,f(
时,f( )=
)= +
+ +a+2≥0
+a+2≥0∴
 .
.综上所述,a的最小值-
 .
.故选B.
点评:本题考查二次函数的性质和应用,解题时要认真审题,仔细解答,注意对称轴性质的合理运用.

练习册系列答案
相关题目