题目内容
【题目】四棱锥S-ABCD中,底面ABCD为平行四边形,侧面![]() 底面ABCD,已知
底面ABCD,已知![]() ,
,![]() 为正三角形.
为正三角形.
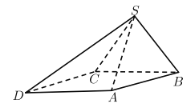
(1)证明![]() .
.
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小的余弦值.
的大小的余弦值.
【答案】(1)证明见解析.(2)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
(1)作![]() 于点
于点![]() ,连接
,连接![]() ,根据面面垂直性质可得
,根据面面垂直性质可得![]() 底面ABCD,由三角形全等性质可得
底面ABCD,由三角形全等性质可得![]() ,进而根据线面垂直判定定理证明
,进而根据线面垂直判定定理证明![]() 平面
平面![]() ,即可证明
,即可证明![]() .
.
(2)根据所给角度和线段关系,可证明以![]() 均为等边三角形,从而取
均为等边三角形,从而取![]() 中点
中点![]() ,连接
,连接![]() ,即可由线段长结合余弦定理求得二面角
,即可由线段长结合余弦定理求得二面角![]() 的大小.
的大小.
(1)证明:作![]() 于点
于点![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
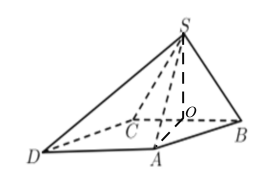
因为侧面![]() 底面ABCD,
底面ABCD,
则![]() 底面ABCD,
底面ABCD,
因为![]() 为正三角形,则
为正三角形,则![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() ,
,
所以![]() ,而
,而![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() .
.
(2)由(1)可知![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() 为
为![]() 中点.
中点.
由等腰三角形三线合一可知![]() ,
,
在![]() 中,由等腰三角形三线合一可得
中,由等腰三角形三线合一可得![]() ,
,
所以![]() 均为边长为2的等边三角形,
均为边长为2的等边三角形,
取![]() 中点
中点![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
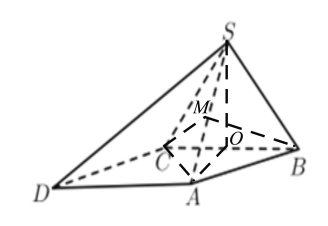
由题意可知,![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
所以在![]() 中由余弦定理可得
中由余弦定理可得
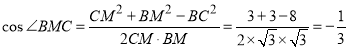 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: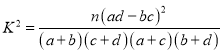 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
