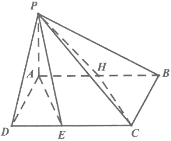
题目内容
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,上顶点为
,上顶点为![]() ,原点O到直线
,原点O到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)若点T在圆![]() 上,点A为椭圆的右顶点,是否存在过点A的直线l交椭圆C于点B(异于点A),使得
上,点A为椭圆的右顶点,是否存在过点A的直线l交椭圆C于点B(异于点A),使得![]() 成立?若存在,求出直线l的方程;若不存在,请说明理由.
成立?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】(1) ![]() (2) 存在满足条件的直线
(2) 存在满足条件的直线![]() ,其方程为
,其方程为![]() .
.
【解析】
(1)根据条件列方程组,解得![]() 即可,(2)设直线方程,与椭圆方程联立方程组,利用韦达定理解得B点坐标,再根据条件得T点坐标,代入圆方程,解得直线斜率,即得结果.
即可,(2)设直线方程,与椭圆方程联立方程组,利用韦达定理解得B点坐标,再根据条件得T点坐标,代入圆方程,解得直线斜率,即得结果.
解:(1)由椭圆的一个焦点为![]() 知:
知:![]() ,即
,即![]() .①.
.①.
又因为直线![]() 的方程为
的方程为![]() ,即
,即![]() ,所以
,所以![]() .
.
由①解得![]() .
.
故所求椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)假设存在过点![]() 的直线
的直线![]() 适合题意,则结合图形易判断知直线
适合题意,则结合图形易判断知直线![]() 的斜率必存在,
的斜率必存在,
于是可设直线![]() 的方程为
的方程为![]() ,
,
由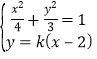 ,得
,得![]() .(*)
.(*)
因为点![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个交点,且
的一个交点,且![]()
所以![]() ,所以
,所以![]() ,
,
即点![]() .
.
所以![]() ,即
,即![]() .
.
因为点![]() 在圆
在圆![]() 上,所以
上,所以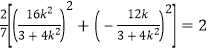 ,
,
化简得![]() ,解得
,解得![]() ,所以
,所以![]() .
.
经检验知,此时(*)对应的判别式![]() ,满足题意.
,满足题意.
故存在满足条件的直线![]() ,其方程为
,其方程为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研究投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:
试销价格 |
|
|
|
|
|
|
产品销量 |
|
|
|
|
|
|
已知变量![]() ,
,![]() 具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>
具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?求回归方程。
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取3个,求“理想数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: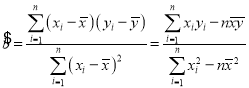 ,
,![]() .
.