题目内容
已知角a为三角形的一个内角,且满足sinatana<0,则角a是第分析:根据 角a为三角形的一个内角,可得0<a<π,又sinatana<0,故有
<a<π,从而得到结论.
| π |
| 2 |
解答:解:∵角a为三角形的一个内角,∴0<a<π,又sinatana<0,∴
<a<π,
故角a是第二象限角,
故答案为二.
| π |
| 2 |
故角a是第二象限角,
故答案为二.
点评:本题考查三角形内角和定理,以及三角函数在各个象限中的符号,判断
<a<π,是解题的关键.
| π |
| 2 |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
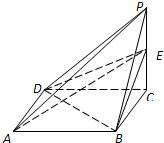
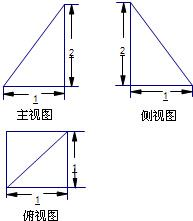
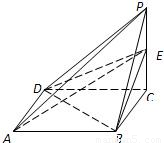
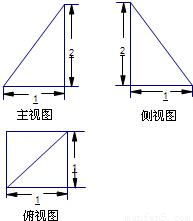
 (3)试探究在DE上是否存在点Q,使得AQ
(3)试探究在DE上是否存在点Q,使得AQ