题目内容
设 是曲线
是曲线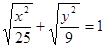 上的点,
上的点,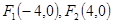 ,则( )
,则( )
A.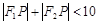 | B.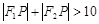 |
C.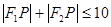 | D.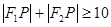 |
A
解析试题分析:因为条件给定 是曲线
是曲线 上的点,那么可知由于点P在椭圆的内部点,那么其到
上的点,那么可知由于点P在椭圆的内部点,那么其到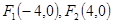 的距离和小于2a=10,只有点在直线的交点处时,表示的满足距离和为10,但是
的距离和小于2a=10,只有点在直线的交点处时,表示的满足距离和为10,但是 ,因此答案选A.
,因此答案选A.
考点:本试题考查了直线的方程与椭圆方程的知识点。
点评:解决该试题的关键是理解椭圆方程的特点和直线方程的特点,然后利用其椭圆的的定义判定不等式的关系式,考查了分析问题和解决问题的能力,属于中档题。

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
两圆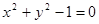 和
和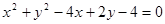 的位置关系是
的位置关系是
| A.内切 | B.相交 | C.外切 | D.外离 |
q是第三象限角,方程x2+y2sinq=cosq表示的曲线是( )
| A.焦点在y轴上的双曲线 | B.焦点在y轴上的椭圆 |
| C.焦点在x轴上的双曲线 | D.焦点在x轴上的椭圆 |
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
已知双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,则满足△
,则满足△ 的周长为
的周长为 的动点
的动点 的轨迹方程为 ( )
的轨迹方程为 ( )
A. | B. | C. | D. |
如果方程 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则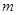 的取值范围是
的取值范围是
A. | B. | C. | D. |
已知椭圆 和双曲线
和双曲线 有公共的焦点,那么双曲线的渐近线方程是( )
有公共的焦点,那么双曲线的渐近线方程是( )
A. | B. | C.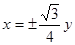 | D. |
 为一个焦点的椭圆,近地点A距地面为
为一个焦点的椭圆,近地点A距地面为 千米,远地点B距地面为
千米,远地点B距地面为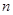 千米,地球半径为
千米,地球半径为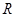 千米,则飞船运行轨道的短轴长为( )
千米,则飞船运行轨道的短轴长为( )
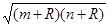

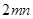
 的焦点为F,准线为l,点P为抛物线上一点,且
的焦点为F,准线为l,点P为抛物线上一点,且 ,垂足为A,若直线AF的斜率为
,垂足为A,若直线AF的斜率为 ,则|PF|等于( )
,则|PF|等于( )
