题目内容
已知数列{an}中,a1=1,a2n+1+an2+1=2(an+1an+an+1-an),求数列 的前n项和Sn.
的前n项和Sn.
解:∵an+12+an2+1=2(an+1an+an+1-an)
∴an+12-2an+1•an+an2-2(an+1-an)+1=0
∴(an+1-an)2-2(an+1-an)+1=0
∴(an+1-an-1)2=0
∴an+1-an=1∴{an}为等差数列
∴an=a1+(n-1)•1=n
∴Sn=
=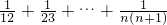
=1- +
+ -
- +…+
+…+ -
- =1-
=1- =
=
分析:本题要根据所给条件,化简整理,得出数列{an}是等差数列并求出通项,数列{ }的和用裂项法即可求得.
}的和用裂项法即可求得.
点评:本题考查了分析运算能力,以及数列求和的方法.分析得出数列是等差数列,会用裂项法求和是关键.
∴an+12-2an+1•an+an2-2(an+1-an)+1=0
∴(an+1-an)2-2(an+1-an)+1=0
∴(an+1-an-1)2=0
∴an+1-an=1∴{an}为等差数列
∴an=a1+(n-1)•1=n
∴Sn=

=
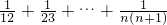
=1-
 +
+ -
- +…+
+…+ -
- =1-
=1- =
=
分析:本题要根据所给条件,化简整理,得出数列{an}是等差数列并求出通项,数列{
 }的和用裂项法即可求得.
}的和用裂项法即可求得.点评:本题考查了分析运算能力,以及数列求和的方法.分析得出数列是等差数列,会用裂项法求和是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|