题目内容
(本小题满分12分)
设函数 的定义域为集合
的定义域为集合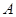 ,不等式
,不等式 的解集为集合
的解集为集合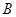 .
.
(1)求集合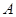 ,
,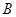 ;
;
(2)求集合 ,
, .
.
(1)  ,
,
(2)  ,
, 或
或
解析试题分析:解:(1)由 ,得
,得 ,∴
,∴
由 ,即
,即
得 ,解得
,解得
∴
(2)
∵ 或
或
∴ 或
或
考点:函数定义域和不等式的解集
点评:解决的关键是能结合函数定义域以及对数函数单调性来得到不等式的解集,进而得到集合A,B,然后结合补集和交集的思想来求解,属于基础题。

练习册系列答案
相关题目
题目内容
(本小题满分12分)
设函数 的定义域为集合
的定义域为集合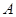 ,不等式
,不等式 的解集为集合
的解集为集合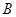 .
.
(1)求集合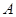 ,
,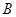 ;
;
(2)求集合 ,
, .
.
(1)  ,
,
(2)  ,
, 或
或
解析试题分析:解:(1)由 ,得
,得 ,∴
,∴
由 ,即
,即
得 ,解得
,解得
∴
(2)
∵ 或
或
∴ 或
或
考点:函数定义域和不等式的解集
点评:解决的关键是能结合函数定义域以及对数函数单调性来得到不等式的解集,进而得到集合A,B,然后结合补集和交集的思想来求解,属于基础题。
