题目内容
设命题p:函数 是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
【答案】分析:命题中,根据指数函数的性质,求出a的范围,对于命题q,根据二次函数的性质,求出a的范围,因为“p且q”为假命题,“p或q”为真命题,得p、q中一真一假,然后再分类讨论;
解答:解:命题p:∵函数 是R上的减函数,
是R上的减函数,
由 得
得 …(3分)
…(3分)
命题q:∵f(x)=(x-2)2-1,在[0,a]上的值域为[-1,3]得2≤a≤4…(7分)
∵p且q为假,p或q为真 得p、q中一真一假.
若p真q假得, …(9分)
…(9分)
若p假q真得, . …(11分)
. …(11分)
综上, <a<2或.
<a<2或. ≤a≤4.…(12分)
≤a≤4.…(12分)
点评:此题主要考查指数函数的性质以及二次函数的性质,以及分类讨论思想的应用,另外计算量比较大要仔细计算;
解答:解:命题p:∵函数
 是R上的减函数,
是R上的减函数,由
 得
得 …(3分)
…(3分)命题q:∵f(x)=(x-2)2-1,在[0,a]上的值域为[-1,3]得2≤a≤4…(7分)
∵p且q为假,p或q为真 得p、q中一真一假.
若p真q假得,
 …(9分)
…(9分)若p假q真得,
 . …(11分)
. …(11分)综上,
 <a<2或.
<a<2或. ≤a≤4.…(12分)
≤a≤4.…(12分)点评:此题主要考查指数函数的性质以及二次函数的性质,以及分类讨论思想的应用,另外计算量比较大要仔细计算;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在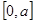 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围. 是R上的减函数,
是R上的减函数, 上的值域为[-1,3],
上的值域为[-1,3], 的取值范围.
的取值范围. 是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围. 是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.