Question

已知△ABC的AB边上的高线所在直线的方程为2x-3y+1=0和AC边上的高线所在的直线方程为x+y=0，顶点A（1，2），求BC边所在直线的方程．

Answer 1

分析：根据点B、C分别在高线所在直线上，设B（-m，m），C（

1

2

（3n-1），n），由直线的垂直关系和斜率公式建立关于m、n的方程组，解出m=-7且n=-1，得到B、C两点的坐标．再利用直线的两点式列式，化简即得BC边所在直线的方程．

解答：解：根据题意，设AB边上的高为CE，AC边上的高为BD

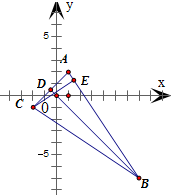
设B（-m，m），C（

1

2

（3n-1），n）
可得k_AC=

n-2

1 2 (3n-1)-1

=

-1

-1

=1，解之得n=-1，得C（-2，-1）
k_AB=

m-2

-m-2

=

-1

2 3

=-

3

2

，解之和m=-7，得B（7，-7）
因此，直线BC的方程为

y+1

-7+1

=

x+2

7+2

，化简得2x+3y+7=0．

点评：本题给出三角形的一个顶点坐标，在已知两条高线的方程情况下求边所在直线方程．着重考查了直线的基本量与基本形式和直线的位置关系等知识，属于中档题．