题目内容
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动.若厂家投放A、B型号电视机的价值分别为p、q万元,农民购买电视机获得的补贴分别为| 1 |
| 10 |
| 2 |
| 5 |
分析:先设B型号电视机的价值为x万元(1≤x<9),农民得到的补贴为y万元,由题意得,函数y的表达式,再利用导数求出此函数的最大值,从而得到分配方案,求出最大值.
解答:解:设B型号电视机的价值为x万元(1≤x<9),农民得到的补贴为y万元,
则A型号电视机的价值为(10-x)万元,
由题意得,
y=
(10-x)+
lnx=
lnx-
x+1
y′=
-
由y′=0得,x=4
当x∈[1,4)时,y′>0,
当x∈(4,9]时,y′<0
所以当x=4时,y取最大值,
ymax=
ln4-0.4+1≈1.2
即厂家分别投放A、B两型号电视机6万元和4万元时,农民得到补贴最多,最多补贴约1.2万元.
则A型号电视机的价值为(10-x)万元,
由题意得,
y=
| 1 |
| 10 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 10 |
y′=
| 2 |
| 5x |
| 1 |
| 10 |
由y′=0得,x=4
当x∈[1,4)时,y′>0,
当x∈(4,9]时,y′<0
所以当x=4时,y取最大值,
ymax=
| 2 |
| 5 |
即厂家分别投放A、B两型号电视机6万元和4万元时,农民得到补贴最多,最多补贴约1.2万元.
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.其中利用导数求函数的最值是解题的关键.

练习册系列答案
相关题目
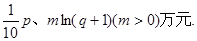 已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据:
已知厂家把价值为10万元的A、B两种型号的电视机投放市场,且A、B两种型号的电视机投放金额都不低于1万元(精确到0.1,参考数据: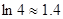 ).
).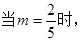 请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值;
请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值; 万元.已知厂家把总价值为10万元的A、B两种型号电视机投放电场,且A、B型号的电视机投放金额不低于1万元,请你制订一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:ln4=1.4)
万元.已知厂家把总价值为10万元的A、B两种型号电视机投放电场,且A、B型号的电视机投放金额不低于1万元,请你制订一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值(精确到0.1,参考数据:ln4=1.4)