题目内容

已知x，y满足条件
x+y+2＞0
x+2y+1≤0
y≥0.
则r=（x-1）2+（y-2）2的值域是
 
．
分析：先根据约束条件画出可行域，设r=（x-1）2+（y-2）2，再利用r的几何意义求最值，只需求出点P（1，2）与可行域内的点的距离的最值即得．
解答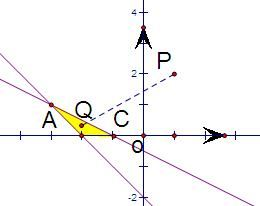：精英家教网 解：先根据约束条件画出可行域，
设r=（x-1）2+（y-2）2，
表示可行域内点到点P（1，2）距离的平方，
当在点A时，r最大，最大值为（1+3）2+（2-1）2=17，
当在点C时，r最小，最小值为（1+1）2+（2-0）2=8，
故答案为：[8，17）．
点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．
练习册系列答案
相关题目
已知x，y满足条件
x-y+5≥0
x+y≥0
x≤3
，则z=
x+y+2
x+3
的最小值（（　　）
A、4
B、
13
6
C、
1
3
D、-
2
3
已知x、y满足条件
x-y+5≥0
x+y≥0
x≤3.
则2x+4y的最小值为（　　）
A、6B、-6C、12D、-12
已知x，y满足条件
x-2y≥0
x+y-3≥0
2x-y-6≤0
，则z=x+2y的最大值（　　）
已知x，y满足条件
x≥0
y≥0
x+y≥2
，则x2+y2的最小值为
2
2
．
已知x，y满足条件
x-y+1≥0
x+y-2≥0
x≤2
，则
2x
4y
的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网