题目内容
(本小题满分13分) 已知函数 ,且
,且 对于任意实数
对于任意实数 ,恒有
,恒有 .
.
(1)求函数 的解析式;
的解析式;
(2)已知函数 在区间
在区间 上单调,求实数
上单调,求实数 的取值范围;
的取值范围;
(3)若函数 有2个零点?求
有2个零点?求 的取值范围.
的取值范围.
 ,且
,且 对于任意实数
对于任意实数 ,恒有
,恒有 .
.(1)求函数
 的解析式;
的解析式;(2)已知函数
 在区间
在区间 上单调,求实数
上单调,求实数 的取值范围;
的取值范围;(3)若函数
 有2个零点?求
有2个零点?求 的取值范围.
的取值范围.(1)由题设得
 ,
, 因为
 ,
,所以
 ……………………2分
……………………2分所以
 对于任意实数
对于任意实数 恒
恒 成立
成立 .故
.故 ……………………3分
……………………3分(2)由

 ,求导数得
,求导数得 …4分
…4分 在
在 上恒单调,只需
上恒单调,只需 或
或 在
在 上恒成立,即
上恒成立,即 或
或 恒成立,所以
恒成立,所以 或
或 在
在 上恒成立……………………6分
上恒成立……………………6分记
 ,可知:
,可知: ,
, 或
或 ……………………8分
……………………8分(3) 令
 ……9分
……9分令

 ………………………………………11分
………………………………………11分所以当
 时,
时, 有
有 两个零点…..13分
两个零点…..13分略

练习册系列答案
相关题目
 的定义域是 ( )
的定义域是 ( )



 ,则
,则 =( )
=( )



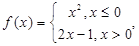 若
若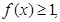 则x的取值范围是
则x的取值范围是



 在
在 上有实根,则
上有实根,则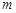 的取值范围是( )
的取值范围是( )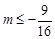



 的值域为
的值域为 ,且
,且 ,则
,则 的最大值为( )
的最大值为( )
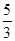


 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.  (万元)与每件产品的售价
(万元)与每件产品的售价
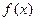 的定义域为
的定义域为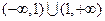 ,且
,且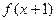 为奇函数,当
为奇函数,当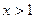 时,
时, 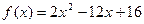 ,则直线
,则直线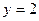 与函数
与函数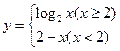 ,右下图表示的是给定
,右下图表示的是给定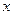 的值,求其
的值,求其 对应的函数值
对应的函数值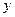 的程序框图,①处应填写 ;
的程序框图,①处应填写 ; 应填写 。
应填写 。