Question

【题目】已知f（x）= sinxcosx+cos2x，锐角△ABC的三个角A，B，C所对的边分别为a，b，c． （Ⅰ）求函数f（x）的最小正周期和单调递增区间；
（Ⅱ）若f（C）=1，求m= 的取值范围．

Answer 1

【答案】解：（Ⅰ） ．∴函数f（x）的最小正周期 ．
由 是单调递增，
解得： ．
∴函数f（x）的单调递增区间 ，最小正周期为π．
（Ⅱ）由（Ⅰ）可得f（C）=sin（2C+ ）=1
∴ ．
∴
∴ 或 k∈Z，
∵△ABC是锐角三角形，
∴ ．
由余弦定理c2=a2+b2﹣2abcosC，可得c2=a2+b2﹣ab
∴ ．
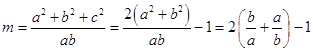∵△ABC为锐角三角形
∴ ∴ ．
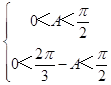由正弦定理得： ．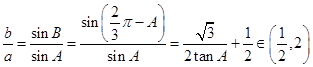
∴
【解析】（Ⅰ）将f（x）化简，结合三角函数的性质求解即可．（Ⅱ）利用f（C）=1，求解角C，由余弦定理建立等式关系，利用三角函数的有界限求解范围．