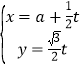题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在
在![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判断四边形
,判断四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)根据离心率和椭圆经过的点的坐标,建立方程组求解椭圆的方程;(2)写出四边形的面积表达式,结合表达式的特征进行判断.
解:(1)因为椭圆![]() 的离心率
的离心率![]() ,所以
,所以![]() ,即
,即![]() .
.
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .
.
由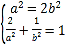 ,
,
解得![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() 或
或![]() ,此时四边形
,此时四边形![]() 的面积为
的面积为![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程是
的方程是![]() ,
,
联立方程组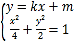 ,消去
,消去![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
由![]() ,得
,得![]() ,
,![]() .
.
因为点![]() 在曲线
在曲线![]() 上,所以有
上,所以有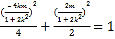 ,整理得
,整理得![]() .
.
由题意,四边形![]() 为平行四边形,所以四边形
为平行四边形,所以四边形![]() 的面积为
的面积为
![]()
![]() .
.
由![]() ,得
,得![]() ,故四边形
,故四边形![]() 的面积是定值,其定值为
的面积是定值,其定值为![]() .
.

练习册系列答案
相关题目
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.