题目内容
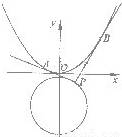
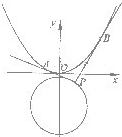 如图,设点
如图,设点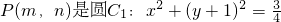 上的动点,过点P作抛物线
上的动点,过点P作抛物线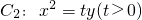 的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.
的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.
(I)求t的值;
(Ⅱ)求 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标.
解:(Ⅰ)圆C1的圆心M(0,-1),抛物线C2的准线为y=- ,
,
∵圆C1的圆心M在抛物线C2的准线上,∴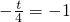 ,解得t=4.
,解得t=4.
∴t的值为4.
(Ⅱ)由题意可知:切线PA、PB的斜率都存在,分别为k1,k2,切点A(x1,y1),B(x2,y2).
设过点P的抛物线的切线l:y=k(x-m)+n,代入x2=4y,
可得x2-4kx+(4km-4n)=0(*)
∵直线l与抛物线相切,∴△=16k2-4×(4km-4n)=0,化为k2-km+n=0.
∴k1+k2=m,k1k2=n.(**)
此时,x1=2k1,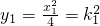 ;同理,x2=2k2,
;同理,x2=2k2,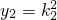 .
.
∴ =(x1-m)(x2-m)+(y1-n)(y2-n)
=(x1-m)(x2-m)+(y1-n)(y2-n)
=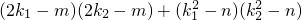
=4k1k2-2m(k1+k2)+ -
-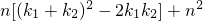
=4n-2m2+m2+n2-n(m2-2n)+n2
=4n2+4n-m2(1+n).
∵点P(m,n)在圆C1上,∴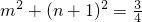 ,∴
,∴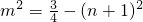 ,代入上式可得
,代入上式可得
 =
=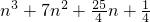 ,
,
考查函数f(n)=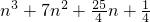
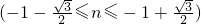 .
.
求得f′(n)=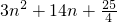 =
=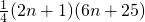 ,
,
令f′(n)=0,解得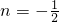 或
或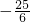 .
.
当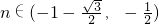 时,f′(n)<0,f(n)单调递减;
时,f′(n)<0,f(n)单调递减;
当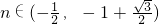 时,f′(n)>0,f(n)单调递增.
时,f′(n)>0,f(n)单调递增.
∴当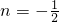 时,f(n)取得最小值
时,f(n)取得最小值 .
.
此时对应的点P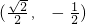 .
.
分析:(Ⅰ)先分别求出圆心坐标和抛物线的准线方程,进而即可得出;
(Ⅱ)设出切线的方程,并与抛物线的方程联立,由相切可得△=0,利用根与系数的关系及数量积即可得出 ,再利用点P在圆上及函数的导数即可求出最小值.
,再利用点P在圆上及函数的导数即可求出最小值.
点评:熟练掌握圆锥曲线的定义与性质、直线与圆锥曲线相切问题的解决模式、根与系数的关系、利用导数求函数的最值等是解题的关键.
 ,
,∵圆C1的圆心M在抛物线C2的准线上,∴
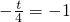 ,解得t=4.
,解得t=4.∴t的值为4.
(Ⅱ)由题意可知:切线PA、PB的斜率都存在,分别为k1,k2,切点A(x1,y1),B(x2,y2).
设过点P的抛物线的切线l:y=k(x-m)+n,代入x2=4y,
可得x2-4kx+(4km-4n)=0(*)
∵直线l与抛物线相切,∴△=16k2-4×(4km-4n)=0,化为k2-km+n=0.
∴k1+k2=m,k1k2=n.(**)
此时,x1=2k1,
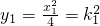 ;同理,x2=2k2,
;同理,x2=2k2,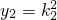 .
.∴
 =(x1-m)(x2-m)+(y1-n)(y2-n)
=(x1-m)(x2-m)+(y1-n)(y2-n)=
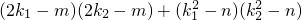
=4k1k2-2m(k1+k2)+
 -
-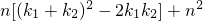
=4n-2m2+m2+n2-n(m2-2n)+n2
=4n2+4n-m2(1+n).
∵点P(m,n)在圆C1上,∴
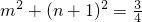 ,∴
,∴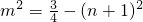 ,代入上式可得
,代入上式可得 =
=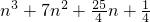 ,
,考查函数f(n)=
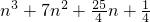
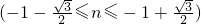 .
.求得f′(n)=
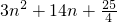 =
=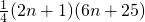 ,
,令f′(n)=0,解得
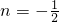 或
或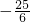 .
.当
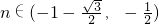 时,f′(n)<0,f(n)单调递减;
时,f′(n)<0,f(n)单调递减;当
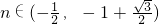 时,f′(n)>0,f(n)单调递增.
时,f′(n)>0,f(n)单调递增.∴当
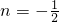 时,f(n)取得最小值
时,f(n)取得最小值 .
.此时对应的点P
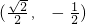 .
.分析:(Ⅰ)先分别求出圆心坐标和抛物线的准线方程,进而即可得出;
(Ⅱ)设出切线的方程,并与抛物线的方程联立,由相切可得△=0,利用根与系数的关系及数量积即可得出
 ,再利用点P在圆上及函数的导数即可求出最小值.
,再利用点P在圆上及函数的导数即可求出最小值.点评:熟练掌握圆锥曲线的定义与性质、直线与圆锥曲线相切问题的解决模式、根与系数的关系、利用导数求函数的最值等是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
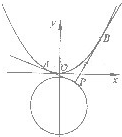 如图,设点
如图,设点 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且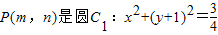 上的动点,过点P作抛物线
上的动点,过点P作抛物线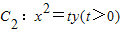 的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.
的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.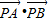 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标.