题目内容
函数y=
的最大值为
.
| sinx-3 |
| cosx+4 |
-12+2
| ||
| 15 |
-12+2
| ||
| 15 |
分析:先将y=
化成sinx-ycosx=4y+3,再利用三角函数的和角公式化成:
sin(x+θ)=4y-3,最后利用三角函数的有界性即可求得值域.
| sinx-3 |
| cosx+4 |
| 1+y2 |
解答:解:∵y=
,∴sinx-3=ycosx+4y,∴sinx-ycosx=4y+3
即
sin(x-θ)=4y-3,其中tanθ=y
∵-
≤
sin(x-θ)≤
∴-
≤4y+3≤
解得
≤y≤
故函数y=
的最大值为:
故答案为:
| sinx-3 |
| cosx+4 |
即
| 1+y2 |
∵-
| 1+y2 |
| 1+y2 |
| 1+y2 |
∴-
| 1+y2 |
| 1+y2 |
解得
-12-2
| ||
| 15 |
-12+2
| ||
| 15 |
故函数y=
| sinx-3 |
| cosx+4 |
-12+2
| ||
| 15 |
故答案为:
-12+2
| ||
| 15 |
点评:本题以三角函数为载体考查分式函数的值域,实质属于求三角函数的最值问题,属基本题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
把函数y=sinx的图象上所有点向右平移
个单位,再将图象上所有点的横坐标缩小到原来的
(纵坐标不变),所得解析式为y=sin(ωx+φ),则( )
| π |
| 3 |
| 1 |
| 2 |
A、ω=2,φ=
| ||||
B、ω=2,φ=-
| ||||
C、ω=
| ||||
D、ω=
|
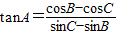 成立,则△ABC为A=60°的三角形.
成立,则△ABC为A=60°的三角形.