Question

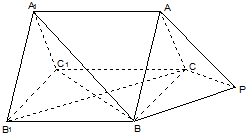如图，已知正三棱柱ABC-A₁B₁C₁中，AB=2

2

，AA₁=2，三棱锥P-ABC中，P∈平面AB₁B₁B，且PA=PB=

3

．
（1）求证：PA∥平面A₁BC₁；
（2）求二面角P-AC-C₁的大小；
（3）求点P到平面BCC₁B₁的距离．

Answer 1

分析：（1）在Rt△ABA₁中，AB=2

2

，AA₁=2，可得cos∠ABA1=

2

3

，取BC中点H，根据题意得：在Rt△PAH中，PH=1，cos∠PAH=

2

3

，所以∠ABA₁=∠PAH进而根据角的关系得到平行关系．
（2）由题意可得：PH⊥平面ABC．过H作HE⊥AC于E，连接PE，则PE⊥AC，∠PEH为二面角P-AC-B的平面角，再结合解三角形的有关知识得到答案．
（3）由PH∥BB₁可得P点到平面BCC₁B₁的距离，就是H到平面BCC₁B₁的距离，再结合题中的条件求出答案．

解答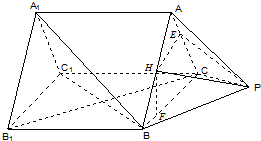：解：（1）证明：在Rt△ABA₁中，AB=2

2

，AA₁=2，
∴cos∠ABA1=

2

3

，取BC中点H，
∵PA=PB，
∴PH⊥AB，
在Rt△PAH中，PH=1，cos∠PAH=

2

3

，又∠ABA₁、∠PAH均为锐角，
∴∠ABA₁=∠PAH，---------------（2分）
∴PA∥A₁B，又PA在平面A₁BC₁外，
∴PA∥平面A₁BC₁．---------------（4分）
（2）∵平面PAB⊥平面ABC，PH⊥AB，
∴PH⊥平面ABC．
过H作HE⊥AC于E，连接PE，则PE⊥AC，∠PEH为二面角P-AC-B的平面角，------------------------（6分）
由题意可得：HE=

1

2

•(

3

2

•2

2

)=

6

2

，
∴tan∠PEH=

PH

HE

=

6

3

，
∴二面角P-AC-C₁的大小为

π

2

+arctan

6

3

．------------------------（9分）
（3）∵PH∥BB₁，
∴P点到平面BCC₁B₁的距离，就是H到平面BCC₁B₁的距离，-------------------------------（11分）
过H作HF⊥BC于F，则HF⊥平面BCC₁B₁，HF的长度即为所求，
由题意可得：HF=HE=

6

2

（或用等体积VP-B1BC=VC-B1BP求）----------------------------------（14分）

点评：解决此类问题的关键是熟练掌握几何体的结构特征，进而得到空间中点、线、面的位置关系，结合有关定理进行证明即可，以及熟练掌握求作二面角平面角的方法．