题目内容
已知动点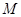 到点
到点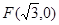 的距离与到直线
的距离与到直线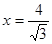 的距离之比为定值
的距离之比为定值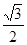 ,记
,记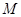 的轨迹为
的轨迹为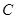 .
.
(1)求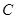 的方程,并画出
的方程,并画出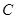 的简图;
的简图;
(2)点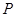 是圆
是圆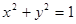 上第一象限内的任意一点,过
上第一象限内的任意一点,过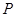 作圆的切线交轨迹
作圆的切线交轨迹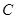 于
于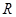 ,
,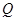 两点.
两点.
(i)证明: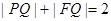 ;
;
(ii)求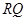 的最大值.
的最大值.
(1)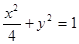 ,C的图象是椭圆.
,C的图象是椭圆.
(2)(i)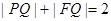 。(ii)当
。(ii)当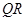 过点
过点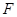 时取最大值2
时取最大值2
解析试题分析:(1)设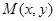 ,由题动点M满足:
,由题动点M满足: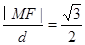 1分
1分
其中: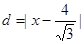 ,
,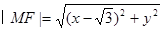
...2分
代入,化简得: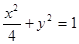
C的图象是椭圆,如图所示. 4分
(2)(i)设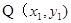 ,
,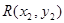
则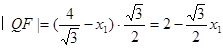 5分
5分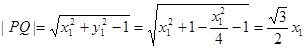 6分
6分
即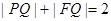 7分
7分
(ii)解法一、设切线为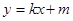 ,由题
,由题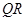 与圆相切,得
与圆相切,得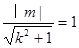 ,
,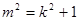
8分
再由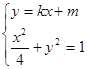 ,得
,得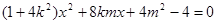 9分
9分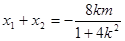 10分
10分
由(i)知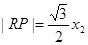 ,所以
,所以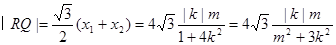
11分
又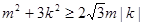 . 2分
. 2分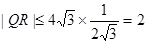 ,当
,当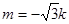 时,取最大值2 13分
时,取最大值2 13分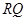 的最大值为2. ...14分
的最大值为2. ...14分
解法二、
由(i)同理得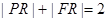 ,则
,则
又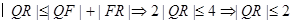
当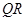 过点
过点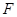 时取最大值2
时取最大值2
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,直线与圆、直线与椭圆的位置关系,弦长公式。
点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。涉及弦长问题,一般要利用韦达定理,简化解题过程。本题“几何味”较浓,应认真分析几何特征。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ,过点
,过点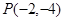 的直线
的直线 的参数方程为
的参数方程为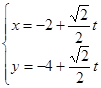 ,设直线
,设直线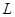 与曲线
与曲线 分别交于
分别交于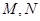 ;
;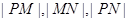 成等比数列,求
成等比数列,求 的值.
的值.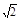 ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-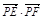 的取值范围.
的取值范围.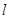 的参数方程为
的参数方程为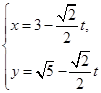 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为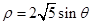 。
。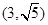 ,求|PA|+|PB|。
,求|PA|+|PB|。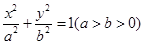 过点
过点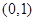 ,其长轴、焦距和短轴的长的平方依次成等差数列.
,其长轴、焦距和短轴的长的平方依次成等差数列.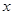 轴正半轴、
轴正半轴、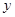 轴分别交于点
轴分别交于点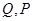 ,与椭圆分别交于点
,与椭圆分别交于点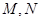 ,各点均不重合,且满足
,各点均不重合,且满足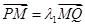 ,
,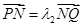 . 当
. 当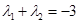 时,试证明直线过定点.过定点(1,0)
时,试证明直线过定点.过定点(1,0)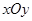 中,点
中,点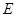 到两点
到两点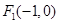 ,
,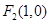 的距离之和为
的距离之和为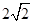 ,设点
,设点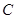 .
. (
(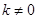 )的直线
)的直线 与曲线
与曲线 ,
, ,点
,点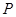 在
在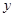 轴上,且
轴上,且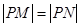 ,求点
,求点 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率为
轴上,离心率为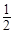 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线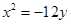 的焦点.
的焦点.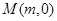 的直线
的直线 与椭圆
与椭圆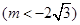 ,直线
,直线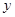 轴交于点
轴交于点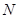 ,当
,当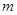 为何值时
为何值时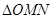 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.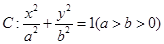 过点
过点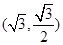 ,椭圆
,椭圆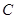 左右焦点分别为
左右焦点分别为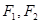 ,上顶点为
,上顶点为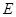 ,
, 为等边三角形.定义椭圆C上的点
为等边三角形.定义椭圆C上的点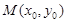 的“伴随点”为
的“伴随点”为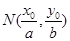 .
. 的最大值;
的最大值; 动圆M与定圆
动圆M与定圆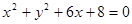 外切且与直线
外切且与直线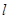 相切.
相切.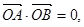 求证直线AB过一定点,并求出定点的坐标.
求证直线AB过一定点,并求出定点的坐标.