题目内容

设函数f（x）=xlnx+（1-x）ln（1-x）（0＜x＜1），求f（x）的最小值．

解：对函数f（x）求导数：f'（x）=（xlnx）'+[（1-x）ln（1-x）]'=lnx-ln（1-x）= $\text{[math]}$ ．
令f^′（x）=0，则 $\text{[math]}$ ，解得 $\text{[math]}$ ．
当0＜ $\text{[math]}$ 在区间 $\text{[math]}$ 是减函数，
当1＞ $\text{[math]}$ 在区间 $\text{[math]}$ 是增函数．
所以 $\text{[math]}$ 时取得最小值， $\text{[math]}$ ．
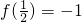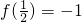分析：利用导数的运算法则即可得到f^′（x），再利用导数与函数单调性、极值与最值的关系即可得到f（x）的最小值．
点评：熟练掌握利用导数研究函数的单调性、极值、最值是解题的关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

已知函数f(x)=x2－1(x≥1)的图象为 C1，曲线C2与C1关于直线y=x对称。

(1)求曲线C2的方程y=g(x)；

(2)设函数y=g(x)的定义域为M，xl，x2∈ M，且xl≠x2，求证|g(x1)－g(x2)|＜|x1－x2|；

(3)设A，B为曲线C2上任意不同两点，证明直线AB与直线y=x必相交。

已知函数f(x)=x2－1(x≥1)的图象为 C1，曲线C2与C1关于直线y=x对称。

(1)求曲线C2的方程y=g(x)；

(2)设函数y=g(x)的定义域为M，xl，x2∈ M，且xl≠x2，求证|g(x1)－g(x2)|＜|x1－x2|；

(3)设A，B为曲线C2上任意不同两点，证明直线AB与直线y=x必相交。

设二次函数f(x)=ax²+bx+c(a≠0)，如果f（x₁）=f(x₂)(x₁≠x₂)，则f(x_l+x₂)等于( )

A．- B．- C.c D．

.(本题满分13分）设函数，方程f(x)=x有唯一的解，

已知f(x_n)=x_n+1(n∈N﹡)且f(x_l)=．

(1)求证：数列{）是等差数列；

(2)若，求Sn=b₁+b₂+b₃+…+b_n

(3)在(2)的条件下，是否存在最小正整数m，使得对任意n∈N﹡，有成立，若存在，求出m的值；若不存在，请说明理由。