Question

已知函数．

（Ⅰ）当a=1时，函数y=f（x）有几个极值点？

（Ⅱ）是否存在实数a，使函数有两个极值？若存在，求实数a的取值范围；若不存在，请说明理由．

Answer 1

考点：

函数在某点取得极值的条件．

专题：

导数的综合应用．

分析：

（Ⅰ）利用导数结合极值的定义即可判断出结论；

（Ⅱ）把问题等价转化，利用导数研究函数的单调性，即可得出结论．

解答：

解：（Ⅰ）当a=1时，函数f（x）=，其定义域为（0，+∞）．

f^′（x）=lnx+1﹣x．

令g（x）=f^′（x）=lnx+1﹣x，则，

令g^′（x）=0，解得x=1．

当0＜x＜1时，g^′（x）＞0，函数g（x）单调递增；当1＜x时，g^′（x）＜0，函数g（x）单调递减．

∴当x=1时，函数g（x）取得极大值，也即最大值，∴g（x）≤g（1）=0，即f^′（x）≤0．

虽然f^′（1）=0，但是在x=1的两侧都有f^′（x）＜0，故x=1不是函数f（x）的极值点．

因此函数f（x）没有极值点．

（Ⅱ）f^′（x）=lnx+1﹣ax，

函数f（x）有两个极值⇔f^′（x）=0在（0，∞）上有两个不等实数根，且每一个根两侧导数异号

⇔直线x=a与函数h（x）=由两个交点．

∵，

∴当x∈（0，1）时，h^′（x）＞0，函数h（x）单调递增；

当x∈（1，+∞）时，h^′（x）＜0，函数h（x）单调递减．

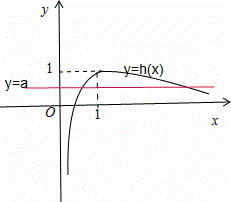
∴当x=1时，函数h（x）取得极大值，也是最大值，画出图象如下：

由图象可知：实数a的取值范围是（0，1）．

点评：

正确把问题等价转化，熟练掌握利用导数研究函数的单调性极值等性质是解题的关键．