题目内容
1．已知函数f（x）=2sinx-t（-$\frac{5π}{2}$≤x≤0）的三个零点x1，x2，x3（x1＜x2＜x3）成等比数列，则log2（-$\sqrt{2}$•t）=（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\sqrt{2}$ |
分析 结合y=sinx的图象可得，则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-3π}\\{{x}_{2}+{x}_{3}=-π}\\{{x}_{2}^{2}={x}_{1}{x}_{2}}\end{array}\right.$，解得x2=-$\frac{3π}{4}$，求出t的值，从而求得log2（-$\sqrt{2}$•t）的值
解答 解：f（x）=2sinx-t（-$\frac{5π}{2}$≤x≤0）的三个零点x1，x2，x3（x1＜x2＜x3）成等比数列
结合y=sinx的图象可得，
则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-3π}\\{{x}_{2}+{x}_{3}=-π}\\{{x}_{2}^{2}={x}_{1}{x}_{2}}\end{array}\right.$，解得x2=-$\frac{3π}{4}$，
∴t=2sin（-$\frac{3π}{4}$）=-$\sqrt{2}$，
∴log2（-$\sqrt{2}$•t）=log22=1，
故选：C
点评 本题考查了三角函数的图象性质，以及等比数列的性质应用，属于中档题．
练习册系列答案
相关题目
14．已知a＞0且a≠1，则（a-1）b＜0是ab＜1的（ ）
| A． | 充要条件 | B． | 必要而不充分条件 | ||
| C． | 充分而不必要条件 | D． | 既不充分也不必要条件 |
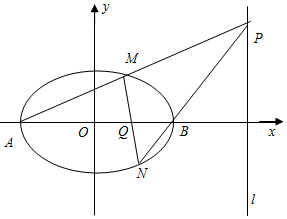在平面直角坐标系xOy中，已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点，离心率为$\frac{1}{2}$，且椭圆过定点$（1，\frac{3}{2}）$，P为椭圆右准线上任意一点，直线PA，PB分别交椭圆于M，N．
13．设α，β是两个不同的平面，m是一条直线，给出下列命题：①若m⊥α，m?β，则α⊥β；②若m∥α，α⊥β，则m⊥β．则（ ）
| A． | ①②都是假命题 | B． | ①是真命题，②是假命题 | ||
| C． | ①是假命题，②是真命题 | D． | ①②都是真命题 |