题目内容

若集合M={（x，y）|x+y=0}，P={（x，y）|x-y=2}，则M∩P=

A.
（1，-1）
B.
{x=1}∪{y=-1}
C.
{1，-1}
D.
{（1，-1）}

D
分析：由题意可得集合P∩M 即两条直线的交点，解方程组 $\text{[math]}$ ，可得两条直线的交点的坐标，从而求得集合P∩M．
解答：集合P和M分别表示直线，集合P∩M 即两条直线的交点，解方程组 $\text{[math]}$ ，
解得： $\text{[math]}$
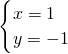
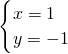
故集合P∩M={（1，-1）}，
故选D．
点评：本题主要考查求两条直线的交点坐标的方法，二元一次方程组的解法，两个集合的交集的定义和求法，属于基础题．

练习册系列答案

天府数学系列答案

天府前沿系列答案

文科爱好者系列答案

理科爱好者系列答案

新学案同步导与练系列答案

名师大课堂系列答案

351高效课堂导学案系列答案

状元成才路状元导练系列答案

快乐小博士巩固与提高系列答案

探究乐园高效课堂系列答案

相关题目

（1）求函数g（x）的解析式．
（2）若集合M={f（x）|f（x）+f（x+2）=f（x+1），x∈R}，试判断g（x）与集合M的关系．
（3）记A={x|a≥2^g（x）}，B={x|y=

3	x2-x-2

(a-5)x2+2(a-5)x-4

}，若（?_RA）∪（?_RB）=∅，求实数a的取值范围．

集合M={1，x，y}，N={x²，x，xy}，若M=N，求x，y的值．

已知集合M={f（x）|y=f（x）}，其元素f（x）须同时满足下列三个条件：
①定义域为（-1，1）；
②对于任意的x，y∈（-1，1），均有f(x)+f(y)=f(

)；
③当x＜0时，f（x）＞0．
（Ⅰ）若函数f（x）∈M，证明：y=f（x）在定义域上为奇函数；
（Ⅱ）若函数h(x)=ln

，判断是否有h（x）∈M，说明理由；
（Ⅲ）若f（x）∈M且f(-

)=1，求函数y=f(x)+

的所有零点．

若所有形如a+

b（a∈Q、b∈Q）的数组成集合M，对于x=

π，则有（）
A．x∈M，y∈M
B．x∈M，y∉M
C．x∉M，y∈M
D．x∉M，y∉M

已知集合M={f（x）|y=f（x）}，其元素f（x）须同时满足下列三个条件：
①定义域为（-1，1）；
②对于任意的x，y∈（-1，1），均有

；
③当x＜0时，f（x）＞0．
（Ⅰ）若函数f（x）∈M，证明：y=f（x）在定义域上为奇函数；
（Ⅱ）若函数

，判断是否有h（x）∈M，说明理由；
（Ⅲ）若f（x）∈M且

的所有零点．