题目内容
已知Sn是数列{an}的前n项的和,对任意的n∈N*,都有Sn=2an-1,则S10=________.
1023
分析:根据an= 及Sn=2an-1,代入即可求得数列{an}的通项公式,根据通项公式代入Sn=2an-1,求出Sn,令n=10,即可求得S10.
及Sn=2an-1,代入即可求得数列{an}的通项公式,根据通项公式代入Sn=2an-1,求出Sn,令n=10,即可求得S10.
解答:当n=1时,得a1=1,
当n≥2时,Sn-1=2an-1-1,①
Sn=2an-1.②
②-①,得an=2an-1,即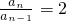 .
.
又∵ ,
,
∴{an}是以1为首项,2为公比的等比数列.
∴ .
.
点评:此题是个中档题.考查根据an= 求数列通项公式的方法以及等比数列的定义,体现了分类讨论的思想.以及学生综合运用知识解决问题的能力.
求数列通项公式的方法以及等比数列的定义,体现了分类讨论的思想.以及学生综合运用知识解决问题的能力.
分析:根据an=
 及Sn=2an-1,代入即可求得数列{an}的通项公式,根据通项公式代入Sn=2an-1,求出Sn,令n=10,即可求得S10.
及Sn=2an-1,代入即可求得数列{an}的通项公式,根据通项公式代入Sn=2an-1,求出Sn,令n=10,即可求得S10.解答:当n=1时,得a1=1,
当n≥2时,Sn-1=2an-1-1,①
Sn=2an-1.②
②-①,得an=2an-1,即
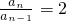 .
.又∵
 ,
,∴{an}是以1为首项,2为公比的等比数列.
∴
 .
.点评:此题是个中档题.考查根据an=
 求数列通项公式的方法以及等比数列的定义,体现了分类讨论的思想.以及学生综合运用知识解决问题的能力.
求数列通项公式的方法以及等比数列的定义,体现了分类讨论的思想.以及学生综合运用知识解决问题的能力. 
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目