题目内容
若双曲线的顶点为椭圆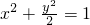 长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是
长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是
- A.x2-y2=1
- B.y2-x2=1
- C.x2-y2=2
- D.y2-x2=2
D
分析:根据椭圆方程求得其长轴的端点坐标和离心率,进而可得双曲线的顶点和离心率,求得双曲线的实半轴和虚半轴的长,进而可得双曲线的方程.
解答:由题意设双曲线方程为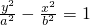 ,离心率为e
,离心率为e
椭圆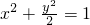 长轴的端点是(0,
长轴的端点是(0, ),所以a=
),所以a= .
.
∵椭圆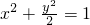 的离心率为
的离心率为
∴双曲线的离心率e= ,?c=2,
,?c=2,
∴b=2,
则双曲线的方程是y2-x2=2.
故选D.
点评:本题主要考查了双曲线的性质和椭圆的标准方程.要记住双曲线和椭圆的定义和性质.
分析:根据椭圆方程求得其长轴的端点坐标和离心率,进而可得双曲线的顶点和离心率,求得双曲线的实半轴和虚半轴的长,进而可得双曲线的方程.
解答:由题意设双曲线方程为
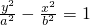 ,离心率为e
,离心率为e椭圆
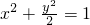 长轴的端点是(0,
长轴的端点是(0, ),所以a=
),所以a= .
.∵椭圆
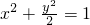 的离心率为
的离心率为
∴双曲线的离心率e=
 ,?c=2,
,?c=2,∴b=2,
则双曲线的方程是y2-x2=2.
故选D.
点评:本题主要考查了双曲线的性质和椭圆的标准方程.要记住双曲线和椭圆的定义和性质.

练习册系列答案
相关题目
 长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是
长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是 B.
B. C.
C. D.
D.
 长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则
长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则 B.
B. C.
C. D.
D.
 长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是
长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是 B.
B. C.
C. D.
D.
 长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是( )
长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程是( ) B.
B. C.
C. D.
D.