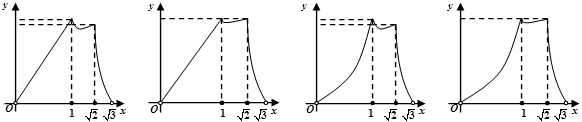题目内容
定义在区间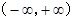 上的奇函数
上的奇函数 为增函数,偶函数
为增函数,偶函数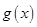 在
在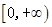 上图象与
上图象与 的图象重合.设
的图象重合.设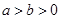 ,给出下列不等式,其中成立的是( )
,给出下列不等式,其中成立的是( )
①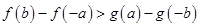
②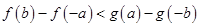
③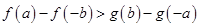
④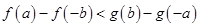
| A.①④ | B.②③ | C.①③ | D.②④ |
C
解析试题分析:因为,定义在区间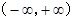 上的奇函数
上的奇函数 为增函数,偶函数
为增函数,偶函数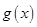 在
在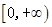 上图象与
上图象与 的图象重合.即偶函数
的图象重合.即偶函数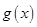 在
在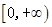 上是增函数,在
上是增函数,在 是减函数。
是减函数。 。
。
当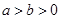 时,
时, ,又
,又
所以,① 故①对②不对.
故①对②不对.
③
故③对④不对.
故选C.
考点:函数的奇偶性、单调性
点评:中档题,此类问题较为典型,比较大小问题,往往利用函数的奇偶性、单调性,必要的话引入“-1,0,1”等作为“媒介”。转化思想很重要。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知偶函数 满足
满足 ,且在区间
,且在区间 上单调递增.不等式
上单调递增.不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
下列函数中既不是奇函数也不是偶函数的是( )
A.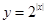 | B.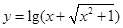 |
C.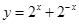 | D.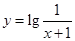 |
函数 是奇函数,图象上有一点为
是奇函数,图象上有一点为 ,则图象必过点( )
,则图象必过点( )
A. | B. | C. | D. |
设函数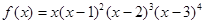 ,则函数
,则函数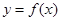 的极大值点为( )
的极大值点为( )
A.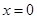 | B.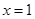 | C.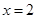 | D.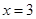 |
函数 的值域是 ( )
的值域是 ( )
A. | B. | C. | D. |
已知函数 是R上的奇函数,若对于
是R上的奇函数,若对于 ,都有
,都有 ,
, 时,
时, 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
函数 的图像与函数
的图像与函数 的图像的交点个数为( )
的图像的交点个数为( )
| A.3 | B.2 | C.1 | D.0 |
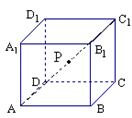
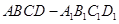 的对角线
的对角线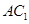 上任取一点P,以
上任取一点P,以 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设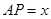 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数