题目内容
将函数f(x)=sin2x-
cos2x的图象向左平移m(m>0)个单位,若所得图象对应的函数为偶函数,则m的最小值是( )
| 3 |
分析:将f(x)=sin2x-
cos2x化为f(x)=2sin(2x-
),再利用函数y=Asin(ωx+φ)的图象变换,结合题意,可求得m的最小值.
| 3 |
| π |
| 3 |
解答:解:∵f(x)=sin2x-
cos2x
=2(
sin2x-
cos2x)
=2sin(2x-
),
将函数f(x)=sin2x-
cos2x的图象向左平移m(m>0)个单位
得到f(x+m)=2sin[2(x+m)-
]=2sin(2x+2m-
),
∵g(x)=f(x+m)=2sin(2x+2m-
)为偶函数,
∴2m-
=kπ+
,k∈Z,
∴m=
+
,k∈Z,
又m>0,
∴mmin=
.
故选:D.
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2sin(2x-
| π |
| 3 |
将函数f(x)=sin2x-
| 3 |
得到f(x+m)=2sin[2(x+m)-
| π |
| 3 |
| π |
| 3 |
∵g(x)=f(x+m)=2sin(2x+2m-
| π |
| 3 |
∴2m-
| π |
| 3 |
| π |
| 2 |
∴m=
| kπ |
| 2 |
| 5π |
| 12 |
又m>0,
∴mmin=
| 5π |
| 12 |
故选:D.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查正弦函数的对称性,突出考查正弦函数与余弦函数的转化,属于中档题.

练习册系列答案
相关题目
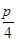 个单位,则所得到的图象对应的函数的一个单调递增区间是
个单位,则所得到的图象对应的函数的一个单调递增区间是 ) C.(
) C.(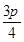 ) D.(
) D.(