题目内容
已知函数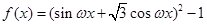 (其中
(其中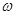 >0),且函数
>0),且函数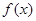 的最小正周期为
的最小正周期为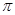 .
.
(Ⅰ)求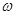 的值;
的值;
(Ⅱ)求函数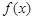 在区间
在区间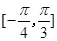 上的最大值和最小值.
上的最大值和最小值.
【答案】
(Ⅰ) 。(Ⅱ)当
。(Ⅱ)当 时,函数取得最小值
时,函数取得最小值 ,
,
当 时,函数取得最大值
时,函数取得最大值 .
.
【解析】
试题分析:(Ⅰ)因为

 2分
2分
 4分
4分
 6分
6分
因为函数 的最小正周期为
的最小正周期为 ,所以
,所以
所以 8分
8分
(Ⅱ)由(Ⅰ)知,函数
当 时,
时, ,
,
所以当 时,函数取得最小值
时,函数取得最小值 11分
11分
当 时,函数取得最大值
时,函数取得最大值 13分
13分
考点:和差倍半的三角函数,正弦型函数的图象和性质。
点评:中档题,本题较为典型,一般的,研究三角函数式的图象和性质,往往需要利用三角公式“化一”,再利用三角函数的图象和性质进一步解题。本题(2)给出角的较小范围,确定三角函数的最值时 ,易于出错,应特别注意。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ·
·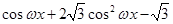 (其中
(其中 >o),且函数
>o),且函数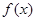 的最小正周期为
的最小正周期为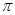
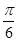 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的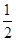 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
 (其中
(其中 >0,
>0, )的最小正周期为
)的最小正周期为 .
. 中,若A<B,且
中,若A<B,且 ,求
,求
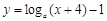 (a > 0,且
(a > 0,且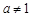 )的图象恒过定点A,若点A在直线
)的图象恒过定点A,若点A在直线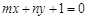 上,其中
上,其中 ,
,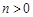 ,则
,则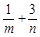 的最小值为__________.
的最小值为__________.