题目内容
15.已知f(x)=log2(4-ax)在区间[-1,3]上是增函数,则a的取值范围是-4<a<0.分析 若f(x)=log2(4-ax)在区间[-1,3]上是增函数,则内函数t=4-ax在区间[-1,3]上是增函数,且恒为正,进而得到答案.
解答 解:∵f(x)=log2(4-ax)在区间[-1,3]上是增函数,
故内函数t=4-ax在区间[-1,3]上是增函数,且恒为正,
故$\left\{\begin{array}{l}-a>0\\ 4+a>0\end{array}\right.$,
解得:-4<a<0,
故答案为:-4<a<0.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质是解答的关键.

练习册系列答案
相关题目
7.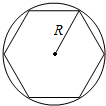 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )| A. | $\frac{3}{2π}$ | B. | $\frac{3\sqrt{3}}{2π}$ | C. | $\frac{3}{4π}$ | D. | $\frac{3\sqrt{3}}{4π}$ |
4.“m=1”是“直线(m-2)x-3my-1=0与直线(m+2)x+(m-2)y+3=0相互垂直”的( )
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |