题目内容
 已知,在
已知,在 中,
中, 是
是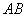 上一点,
上一点, 的外接圆交
的外接圆交 于点
于点 ,
, .(1)求证:
.(1)求证: ;
;
(2)若 平分
平分 ,且
,且 ,求
,求 的长.
的长.
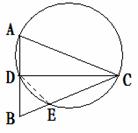 (Ⅰ)连接
(Ⅰ)连接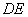 ,因为四边形
,因为四边形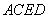 是圆的内接四边形,
是圆的内接四边形,
所以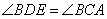 ,又
,又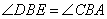 ,
,
所以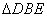 ∽
∽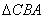 ,即有
,即有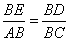 ,
,
又 ,所以
,所以
(Ⅱ)由(Ⅰ)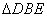 ∽
∽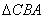 ,知
,知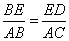 ,
,
又 ,∴
,∴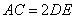 , ∵
, ∵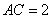 ,∴
,∴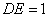 ,而
,而 是
是 的平分线∴
的平分线∴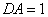 ,设
,设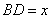 ,根据割线定理得
,根据割线定理得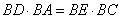
即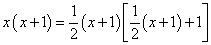 ,解得
,解得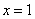 ,即
,即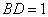

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 的最大值,并写出
的最大值,并写出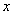 时的取值集合;
时的取值集合;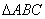 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值. 在函数
在函数 的图象上移动,动点
的图象上移动,动点 满足
满足 ,则动点
,则动点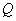 的轨迹方程为( )
的轨迹方程为( ) B.
B. C.
C. D.
D. 

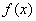 的最大值,并写出
的最大值,并写出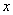 时的取值集合;
时的取值集合; 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值. (B)2 (C)±2
(B)2 (C)±2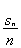 }为等差数列,且通项为
}为等差数列,且通项为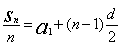 ,类似地,若各项均为正数的等比数列{bn}的首项为b1,公比为q,前n项的积为Tn,则数列{
,类似地,若各项均为正数的等比数列{bn}的首项为b1,公比为q,前n项的积为Tn,则数列{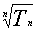 }为等比数列,通项为______________.
}为等比数列,通项为______________. =t1
=t1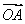 +t2
+t2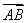 .
.