题目内容
某市有2 100名高中生参加奥林匹克数学竞赛的预选赛（满分10分），随机调阅了60名考生的答卷，得分情况统计如下：得分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数 | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
(1)求样本的平均得分和标准差（精确到0.01);
(2)若总体服从正态分布，求正态曲线的近似方程；
(3)按规定，预赛成绩不低于7分的学生可以参加复赛，试估算进入复赛的人数.
解：(1)平均得分为
=
(4×6+5×15+6×21+7×12+8×3+9×3)=6.样本的方差为
s2=
［6(4-6)2+15(5-6)2+21(6-6)2+12(7-6)2+3(8-6)2+3(9-6)2］=1.5，所以标准差为s=1.22.
(2)以
=6，s=1.22作为总体的平均得分和标准差的估计值，即有μ=6,σ=1.22，则总体服从正态分布N（6，1.222）.因此得正态曲线的近似方程为y=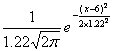
.
(3)F（7）=Φ(
)≈Φ(0.8)=0.788 1.1-F(7)=1-0.788 1=0.211 9.
估计进入复赛的人数为2 100×0.211 9≈445人.
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案某市甲、乙两校高二级学生分别有1100人和1000人，为了解两校全体高二级学生期末统考的数学成绩情况，采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩，并得到成绩频数分布表如下，规定考试成绩在[120，150]为优秀．
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
（1）求表中x与y的值；
（2）由以上统计数据完成下面2x2列联表，问是否有99%的把握认为学生数学成绩优秀与所在学校有关？
| 甲校 | 乙校 | 总计 | |
| 优秀 | a | b | a＋b |
| 非优秀 | c | d | c＋d |
| 总计 | a＋c | b＋d | n |
参考公式：
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
（2）由以上统计数据完成下面2x2列联表，问是否有99%的把握认为学生数学成绩优秀与所在学校有关？
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150） |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
（2）由以上统计数据完成下面2x2列联表，问是否有99%的把握认为学生数学成绩优秀 与所在学校有关？
（3）若以样本的频率作为概率，现从乙校总体中任取 3人（每次抽取看作是独立重复的），求优秀学生人数ξ的分布列和数学期望．（注：概率值可用分数表示）
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |