Question

求圆心在直线3x+4y-1=0上，且经过两圆x²+y²-x+y-2=0与x²+y²=5的交点的圆的方程.

Answer 1

【探究】  先求两圆的交点A、B的坐标，这可以通过解方程组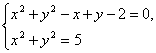得到，之后再利用一般方程或图形的几何特征求解.

以下又可以有两种方法来解决.

解法一：解方程组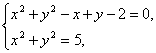得两圆的交点为A(1，-2)和B(2，-1).

设所求圆的方程为x²+y²+Dx+Ey+F=0.

∵A、B在圆上，且圆心(，)在直线3x+4y-1=0上，

∴

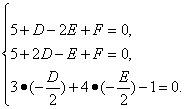
解得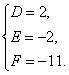

∴所求圆的方程是x²+y²+2x-2y-11=0.

解法二：解方程组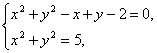得两圆的交点为A(1，-2)和B(2，-1).于是线段AB的垂直平分线方程是x+y=0.

∵圆心在直线3x+4y-1=0上，∴由解得

∴圆心C的坐标是(-1，1).

∵圆的半径r=|AC|=，∴圆的方程是(x+1)²+(y-1)²=13.

【规律总结】 求圆的方程，关键是确定圆心和半径，待定系数法是最常用的方法.解法一利用了一般方程，解法二则直接求出圆心和半径，另外本题也可利用过两圆交点的圆系方程x²+y²+D₁x+E₁y+F₁+λ (x²+y²+D₂x+E₂y+F₂)=0(λ∈R，λ≠-1)，整理成一般式，得到圆心，代入已知直线，建立关于λ的方程，求解后代入所设圆系方程，这种解法思路非常清晰.