题目内容

过点A（2，-1）且被A平分的双曲线 $数学公式$ 的弦所在的直线的方程为

A.
x+2y=0
B.
x-2y-4=0
C.
2x+y-3=0
D.
不存在

D
分析：假设存在，两个交点的坐标分别为（x₁，y₁），（x₂，y₂）所以 $\text{[math]}$ ， $\text{[math]}$ ，两式相减得直线的斜率，进一步求出直线方程，然后联立直线与曲线方程进行检验．
解答：假设存在，两个交点的坐标分别为（x₁，y₁），（x₂，y₂）
所以 $\text{[math]}$
$\text{[math]}$
两式相减得 $\text{[math]}$
所以直线的方程为x+2y=0，
由 $\text{[math]}$ 得：0=4
所以不存在
故选D．
点评：本题主要考查了直线与圆锥曲线的综合问题．解题的关键是充分运用数形结合的数学思想、方程的数学思想和转化的数学思想来解决较为复杂的综合题．

练习册系列答案

晨读晚练系列答案

小学毕业考试试卷精编系列答案

新课程学习资源学习手册系列答案

左记右练系列答案

金钥匙小学毕业总复习系列答案

单元月考卷系列答案

小升初系统总复习指导与检测系列答案

口算达标天天练系列答案

小学毕业升学复习必做的18套试卷系列答案

小桔豆阅读与作文高效训练系列答案

相关题目

过点A（2，-1）且斜率为2的直线的一般式方程为

（2012•浙江模拟）平面内与直线平行的非零向量称为直线的方向向量；与直线的方向向量垂直的非零向量称为直线的法向量．在平面直角坐标系中，利用求动点的轨迹方程的方法，可以求出过点A（2，1）且法向量为

=(-1，2)的直线（点法式）方程为-（x-2）+2（y-1）=0，化简后得x-2y=0．类比以上求法，在空间直角坐标系中，经过点A（2，1，3），且法向量为

=(-1，2，1)的平面（点法式）方程为

（请写出化简后的结果）．

过点A（2，-1）且被A平分的双曲线

-y2=1的弦所在的直线的方程为（　　）

平面内与直线平行的非零向量称为直线的方向向量；与直线的方向向量垂直的非零向量称为直线的法向量．在平面直角坐标系中，利用求动点的轨迹方程的方法，可以求出过点A（2，1）且法向量为 $数学公式$ （点法式）方程为-（x-2）+2（y-1）=0，化简后得x-2y=0．类比以上求法，在空间直角坐标系中，经过点A（2，1，3），且法向量为 $数学公式$ 的平面（点法式）方程为________（请写出化简后的结果）．

平面内与直线平行的非零向量称为直线的方向向量；与直线的方向向量垂直的非零向量称为直线的法向量．在平面直角坐标系中，利用求动点的轨迹方程的方法，可以求出过点A（2，1）且法向量为

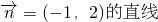（点法式）方程为-（x-2）+2（y-1）=0，化简后得x-2y=0．类比以上求法，在空间直角坐标系中，经过点A（2，1，3），且法向量为

的平面（点法式）方程为（请写出化简后的结果）．