题目内容
函数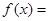
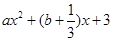 是偶函数,且定义域为
是偶函数,且定义域为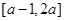 ,则
,则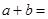 ;
;
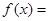
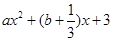 是偶函数,且定义域为
是偶函数,且定义域为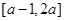 ,则
,则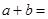 ;
;0
试题分析:根据函数
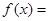
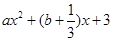 是偶函数,则利用二次函数性质可知,对称轴x=0,则b=-
是偶函数,则利用二次函数性质可知,对称轴x=0,则b=- ,同时由于且定义域为
,同时由于且定义域为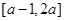 ,则说明1-a="2a,"
,则说明1-a="2a,"  ,综上可知
,综上可知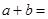 0,故答案为0.
0,故答案为0.点评:解决的关键是根据函数是偶函数确定出参数b的值,然后结合定义域关于原点对称,得到a,b的和值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
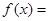
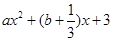 是偶函数,且定义域为
是偶函数,且定义域为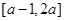 ,则
,则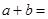 ;
;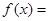
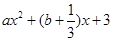 是偶函数,则利用二次函数性质可知,对称轴x=0,则b=-
是偶函数,则利用二次函数性质可知,对称轴x=0,则b=- ,同时由于且定义域为
,同时由于且定义域为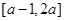 ,则说明1-a="2a,"
,则说明1-a="2a,"  ,综上可知
,综上可知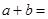 0,故答案为0.
0,故答案为0.
 阅读快车系列答案
阅读快车系列答案