题目内容
已知抛物线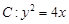 ,的焦点为F,直线
,的焦点为F,直线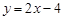 与抛物线C交于A、B两点,则
与抛物线C交于A、B两点,则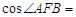 ( )
( )
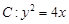 ,的焦点为F,直线
,的焦点为F,直线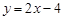 与抛物线C交于A、B两点,则
与抛物线C交于A、B两点,则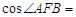 ( )
( )A.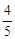 | B.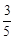 | C. | D. |
C
试题分析:确定抛物线C的焦点F,求出点A,B的坐标,利用求向量夹角余弦值的方法,即可得到答案.根据题意,得到抛物线
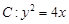 ,的焦点为F,直线
,的焦点为F,直线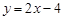 与抛物线C交于A、B两点联立方程组可知,
与抛物线C交于A、B两点联立方程组可知,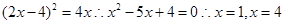 ,那么可知A(1,-2)B(4,4),可得向量的坐标公式,然后借助于向量的数量积来求解可知
,那么可知A(1,-2)B(4,4),可得向量的坐标公式,然后借助于向量的数量积来求解可知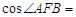
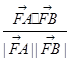 =
= ,故答案为C.
,故答案为C.点评:本题考查的知识点是直线与圆锥曲线的关系,其中构造向量然后利用向量法处理是解答本题的重要技巧

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
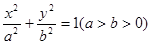 与
与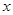 轴负半轴交于点
轴负半轴交于点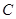 ,
,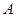 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线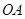 交椭圆于另一点
交椭圆于另一点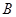 ,椭圆左焦点为
,椭圆左焦点为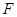 ,连接
,连接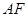 交
交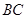 于点D。
于点D。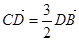 ,求椭圆的离心率;
,求椭圆的离心率; 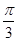 且△ABC的面积为
且△ABC的面积为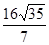 ,求椭圆的标准方程。
,求椭圆的标准方程。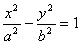
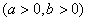 的渐近线与圆
的渐近线与圆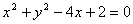 有公共点,则该双曲线的离心率的取值范围是___________.
有公共点,则该双曲线的离心率的取值范围是___________.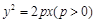 的焦点为
的焦点为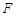 ,过焦点
,过焦点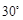 的直线交抛物线于
的直线交抛物线于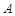 ,
,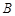 两点,点
两点,点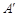 ,
,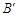 ,若四边形
,若四边形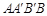 的面积为
的面积为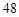 ,则抛物线的方程为____
,则抛物线的方程为____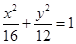 ,则以点
,则以点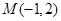 为中点的弦所在直线方程为__________________。
为中点的弦所在直线方程为__________________。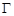 :
: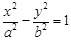
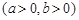 的离心率
的离心率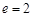 ,过双曲线
,过双曲线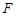 作
作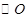 :
: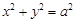 的两条切线,切点分别为
的两条切线,切点分别为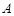 、
、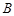 ,则
,则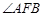 的大小等于( )
的大小等于( )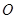 为中心,
为中心,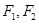 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点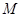 ,满足
,满足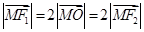 ,则该椭圆的离心率为
,则该椭圆的离心率为
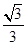
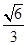

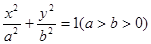 的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=
的两个焦点为F1、F2,点P在椭圆C上,且|PF1|=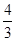 ,
,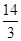 , PF1⊥F1F2.
, PF1⊥F1F2.  =16x
=16x