题目内容
(本小题满分12分)如图,在三棱柱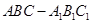 中,
中,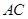 ⊥
⊥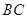 ,
,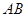 ⊥
⊥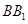 ,
,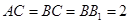 ,
,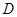 为
为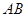 的中点,且
的中点,且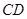 ⊥
⊥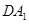 .
.
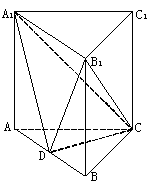
(1)求证: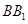 ⊥平面
⊥平面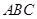 ;(2)求三棱锥
;(2)求三棱锥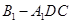 的体积.
的体积.
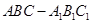 中,
中,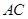 ⊥
⊥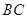 ,
,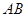 ⊥
⊥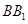 ,
,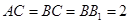 ,
,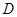 为
为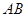 的中点,且
的中点,且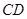 ⊥
⊥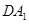 .
.
(1)求证:
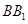 ⊥平面
⊥平面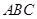 ;(2)求三棱锥
;(2)求三棱锥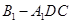 的体积.
的体积.解:(1)见解析;(2)  =
=
 ·CD
·CD
= A1B1×B1B×CD=
A1B1×B1B×CD= ×2
×2 ×2×
×2× =
= .
.
 =
=
 ·CD
·CD=
 A1B1×B1B×CD=
A1B1×B1B×CD= ×2
×2 ×2×
×2× =
= .
.本题考查线线垂直,线面垂直及多面体的体积的求法技巧,转化思想的应用,考查计算能力
(1)证明CD⊥BB1,通过BB1⊥AB,AB∩CD=D,即可证明BB1⊥面ABC
(2)所求的体积进行等价转化可以知道几何体的体积.
解:(1)∵AC=BC,D为AB的中点,∴CD⊥AB,又∵CD⊥DA1,∴CD⊥平面ABB1A1,∴CD⊥BB1,
又BB1⊥AB,AB∩CD=D,∴BB1⊥平面ABC.……6分
(2)由(1)知CD⊥平面AA1B1B,故CD是三棱锥C-A1B1D的高,
在Rt△ACB中,AC=BC=2,∴AB=2 ,CD=
,CD= ,
,
又BB1=2,∴ =
=
 ·CD
·CD
= A1B1×B1B×CD=
A1B1×B1B×CD= ×2
×2 ×2×
×2× =
= .……12分
.……12分
(1)证明CD⊥BB1,通过BB1⊥AB,AB∩CD=D,即可证明BB1⊥面ABC
(2)所求的体积进行等价转化可以知道几何体的体积.
解:(1)∵AC=BC,D为AB的中点,∴CD⊥AB,又∵CD⊥DA1,∴CD⊥平面ABB1A1,∴CD⊥BB1,
又BB1⊥AB,AB∩CD=D,∴BB1⊥平面ABC.……6分
(2)由(1)知CD⊥平面AA1B1B,故CD是三棱锥C-A1B1D的高,
在Rt△ACB中,AC=BC=2,∴AB=2
 ,CD=
,CD= ,
,又BB1=2,∴
 =
=
 ·CD
·CD=
 A1B1×B1B×CD=
A1B1×B1B×CD= ×2
×2 ×2×
×2× =
= .……12分
.……12分
练习册系列答案
相关题目
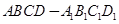 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,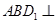 平面
平面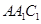
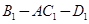 的平面角为120°时,求四棱锥
的平面角为120°时,求四棱锥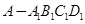 的体积。
的体积。




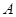 .
.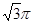
 .
.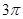
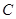 .
.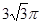
 .
.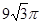
 的外接球
的外接球 的半径为
的半径为 ,且满足
,且满足 ,则正三棱锥
,则正三棱锥







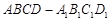 中,
中,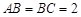 ,过
,过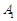 、
、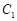 、
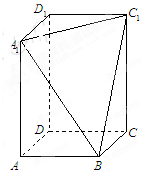
、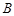 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体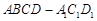 ,且这个几何体的体积为
,且这个几何体的体积为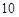 .
.
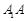 的长;
的长;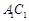 的中点为
的中点为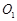 ,求异面直线
,求异面直线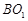 与
与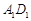 所成角的余弦值.
所成角的余弦值.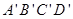 中,AB=1,
中,AB=1,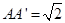 ,则A,C两点间的球面距离为( )
,则A,C两点间的球面距离为( ) 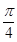
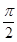
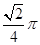
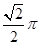
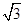 .则正三棱锥S - ABC的外接球的体积为 。
.则正三棱锥S - ABC的外接球的体积为 。