题目内容
(本小题满分12分)已知向量
(Ⅰ)求向量 的长度的最大值;
的长度的最大值;
(Ⅱ)设 ,且
,且 ,求
,求 的值.
的值.

(Ⅰ)求向量
 的长度的最大值;
的长度的最大值;(Ⅱ)设
 ,且
,且 ,求
,求 的值.
的值.(1) 的长度的最大值为2. (2)
的长度的最大值为2. (2)

 的长度的最大值为2. (2)
的长度的最大值为2. (2)

本试题主要是考查了向量的数量积公式的运用,以及两角和差的三角恒等变形,解决三角方程的综合问题。
(1)用坐标关系式表示出向量的模的平方就是向量的平方,借助于向量的数量积得到关于模的长度表示,结合三角函数的张有界性得到最值。
(2)利用向量的垂直关系式,得到数量积为零,那么可知 ,结合方程的知识得到其解。
,结合方程的知识得到其解。
(1)解法1: 则
则


 ,即
,即

当 时,有
时,有 所以向量
所以向量 的长度的最大值为2.
的长度的最大值为2.
解法2: ,
, ,
,


当 时,有
时,有 ,即
,即 ,
,
 的长度的最大值为2.
的长度的最大值为2. 
(2)解法1:由已知可得
 。
。
 ,
, ,即
,即 。
。
由 ,得
,得 ,即
,即 。
。
 ,于是
,于是 。
。
解法2:若 ,则
,则 ,又由
,又由 ,
, 得
得


 ,
, ,即
,即
 ,平方后化简得
,平方后化简得

解得 或
或 ,经检验,
,经检验, 即为所求
即为所求

(1)用坐标关系式表示出向量的模的平方就是向量的平方,借助于向量的数量积得到关于模的长度表示,结合三角函数的张有界性得到最值。
(2)利用向量的垂直关系式,得到数量积为零,那么可知
 ,结合方程的知识得到其解。
,结合方程的知识得到其解。(1)解法1:
 则
则

 ,即
,即

当
 时,有
时,有 所以向量
所以向量 的长度的最大值为2.
的长度的最大值为2.
解法2:
 ,
, ,
,


当
 时,有
时,有 ,即
,即 ,
,  的长度的最大值为2.
的长度的最大值为2. 
(2)解法1:由已知可得

 。
。 ,
, ,即
,即 。
。
由
 ,得
,得 ,即
,即 。
。
 ,于是
,于是 。
。
解法2:若
 ,则
,则 ,又由
,又由 ,
, 得
得

 ,
, ,即
,即
 ,平方后化简得
,平方后化简得

解得
 或
或 ,经检验,
,经检验, 即为所求
即为所求


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,则sin(α-
,则sin(α- )=_____.
)=_____. ,则
,则 =_________.
=_________.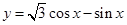 的最大值是 .
的最大值是 . ,tan(β-
,tan(β- )=
)= ,则tan(α+
,则tan(α+ )等于
)等于 



 则
则 等于 .
等于 . 则
则 的值为________________.
的值为________________. 的值是 。
的值是 。