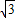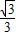Question

已知角α的顶点在原点，始边与x轴的正半轴重合，终边经过点P（-3，

3

）．
（1）求sin2α-tanα的值；
（2）若函数f（x）=cos（x-α）cosα-sin（x-α）sinα，求函数g（x）=

3

f（

π

2

-2x）-2f²（x）在区间[0，

2π

3

]上的最值．

Answer 1

分析：（1）根据三角函数的定义，求出角α的正弦、余弦、正切，再结合二倍角公式，即可得到结论；
（2）先将函数化简，确定角的范围，利用三角函数的性质，即可求得函数的值域．

解答：解：（1）因为角α终边经过点P（-3，

3

），所以sinα=

1

2

，cosα=-

3

2

，tanα=-

3

3

∴sin2α-tanα=2sinαcosα-tanα=-2×

1

2

×

3

2

+

3

3

=-

3

6

（2）∵f（x）=cos（x-α）cosα-sin（x-α）sinα=cosx，x∈R
∴g（x）=

3

cos（

π

2

-2x）+2cos²x=2sin（2x-

π

6

）-1
∵x∈[0，

2π

3

]，∴2x-

π

6

∈[-

π

6

，

7π

6

]
∴sin（2x-

π

6

）∈[-

1

2

，1]
∴2sin（2x-

π

6

）-1∈[-2，1]
∴函数g（x）在区间[0，

2π

3

]上的最小值为-2，最大值为1

点评：本题考查三角函数的定义，考查辅助角公式的而运用，考查三角函数的性质，属于中档题．