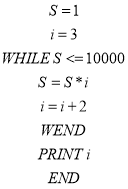题目内容
【题目】已知函数![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,且
内单调递增,且![]() 在
在![]() 上有三个零点,1是其中一个零点.
上有三个零点,1是其中一个零点.
(1)求![]() 的取值范围;
的取值范围;
(2)若直线![]() 在曲线
在曲线![]() 的上方部分所对应的
的上方部分所对应的![]() 的集合为
的集合为![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 无解.
无解.
【解析】试题分析:(1)![]() ,得
,得![]() ,将
,将![]() 的值代入
的值代入![]() 中,将
中,将![]() 代入得到
代入得到![]() 的关系,求出导函数的两个根函数的两个极值点,利用函数的单调性,判断出极值点与单调区间的关系,列出不等式求出
的关系,求出导函数的两个根函数的两个极值点,利用函数的单调性,判断出极值点与单调区间的关系,列出不等式求出![]() 的范围即可;(2)问题转化为
的范围即可;(2)问题转化为![]() 的解集是
的解集是![]() ,根据
,根据![]() 的范围得出矛盾,得到
的范围得出矛盾,得到![]() 的值不存在.
的值不存在.
试题解析: (1)![]() ,
,
因为![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增,
所以![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,
,
于是![]() ,
,
令![]() ,得
,得![]() .
.
因为![]() 在区间
在区间![]() 内单调递增,且
内单调递增,且![]() 在
在![]() 上有三个零点,
上有三个零点,
所以![]() ,
,
所以![]() .
.
(2)由直线![]() 在曲线
在曲线![]() 的上方的部分对应的
的上方的部分对应的![]() 的集合为
的集合为![]() ,
,
得![]() ,即
,即![]() 的解集为
的解集为![]() ,
,
因为![]() 时,
时, ![]() ,
,
而![]() 时,
时, ![]() 必存在正值,
必存在正值,
所以![]() 的解集不可能为
的解集不可能为![]() ,
,
所以![]() 无解.
无解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】学校为了了解高三学生每天自主学习中国古典文学的时间,随机抽取了高三男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据表中数据判断能否有![]() 的把握认为“古文迷”与性别有关?
的把握认为“古文迷”与性别有关?
(2)先从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
(3)现从(2)中所抽取的5人中再随机抽取3人进行体育锻炼时间的调查,记这3人中“古文迷”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
参考公式: 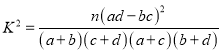 ,其中
,其中![]() .
.